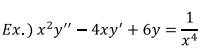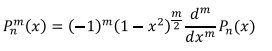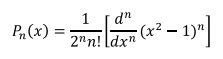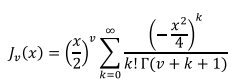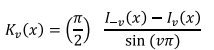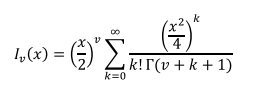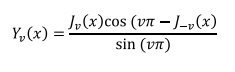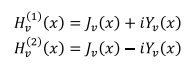معادلات دیفرانسل و تابع بسط در متلب

معادلات دیفرانسل و تابع بسط در متلب

معادلات ديفرانسيل مرتبه دوم

در اين حالت نيزهمانند معادلات مرتبه اول از تابع dsolve استفاده مي کنيم :

> syms x y
>> y=dsolve(‘D2y-Dy-6*y=0′,’x’)
y =
C1*exp(3*x)+C2*exp(-2*x)

> syms x y
>> y=dsolve(‘D2y+2*Dy+2*y=0′,’y(0)=0′,’Dy(0)=-2′,’x’)
y =

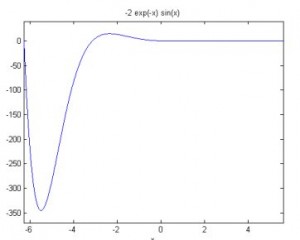
-2*exp(-x)*sin(x)

حال تابع y را رسم مي نماييم :

>> ezplot(y)

> syms x y
>> y=dsolve(‘D2y-2*Dy+y=8+2*x*exp(x)’,’x’)
y =

8+1/3*exp(x)*(3*C2+3*x*C1+x^3)

> syms x y
>> y=dsolve(‘D2y+2*Dy+y=4*(exp(-x))*log(x)’,’x’)
y =
exp(-x)*(C2+x*C1+2*x^2*log(x)-3*x^2)

> syms x y
>> y=dsolve(‘(D2y)*x^2+x*(Dy)-4*y=0′,’x’)
y =
(C1+C2*x^4)/x^2

> syms x y
>> y=dsolve(‘(D2y)*x^2-4*x*(Dy)+6*y=1/(x^4)’,’x’)
y =
1/42*(42*x^7*C2+42*x^6*C1+1)/x^4

معادلات مرتبه n-ام
اين حالت نيزعينا مانند حالات قبل مي باشد :

> syms x y
>> y=dsolve(‘D4y+8*D2y+16*y=-sin(x)’,’x’)
y =
–
1/9*sin(x)+C1*sin(2*x)+C2*cos(2*x)+C3*sin(2*x)*x+C4*cos(2*x)*x

> syms x y
>> y=dsolve(‘x*D3y+D2y=x+1′,’x’)
y =
1/12*x^3+C1*x*log(x)-C1*x+1/2*x^2+C2*x+C3

تذکرمهم : در Matlab منظور از (log(x همان (ln(x مي باشد و (log(x را در Matlab به صورت
(log10(x وارد مي کنند.

> syms x y
>> y=dsolve(‘x^2*D2y-2*x*Dy+2*y=(log(x))^2-log(x^2)’,’x’)
y =

C2*x^2+C1*x-1/2*log(x^2)+1/4+1/2*log(x)^2+3/2*log(x)

> syms x y
>> y=dsolve(‘(x^2-2*x)*D2y+4*(x-1)*Dy+2*y=exp(2*x)’,’x’)
y =
1/4*(4*C2*x+4*C1+exp(2*x))/x/(x-2)

> syms x y
>> y=dsolve(‘(x-1)*D2y-x*Dy+y=0′,’x’)
y =
C1*x+exp(x)*C2

معادله ديفرانسيل لژاندر
معادله ديفرانسيل لژاندر را در حالت کلي بررسي مي نماييم :

syms x y n
>> y=dsolve(‘(1-x^2)*D2y-2*x*Dy+(n)*(n+1)*y=0′,’x’)
y =
C1*LegendreP(n,x)+C2*LegendreQ(n,x)

پس مشاهده مي شود که اين تابع در Matlab تعريف شده مي باشد و به صورت زير مي باشد :

و  تابع چندجمله اي لژاندر از مرتبه n مي باشد و به صورت زيراست :

 

معادله ديفرانسيل بسل
ابتدا معادله را به صورت کلي وارد مي کنيم

syms x y v
>> y=dsolve(‘x^2*D2y+x*Dy+(x^2-v^2)*y=0′,’x’)
y =
C1*besselj(v,x)+C2*bessely(v,x)

مشاهده مي گردد که تابع بسل در Matlab تعريف شده مي باشد :

تابع بسل نوع اول
اين نوع بسل مربوط به معادله زير مي باشد :

در اين حالت تابع بسل به صورت زير تعريف مي گردد :

اگربخواهيم تابع بسل را در يک نقطه حساب کنيم دستور آن به صورت زير مي باشد :

J = besselj(v,x)

مثال : مي خواهيم مقدار را حساب کنيم :

>> J=besselj(5,9)
J =
-0.0550

تابع بسل نوع دوم
اين نوع بسل مربوط به معادله زير مي باشد :

در اين حالت تابع بسل به صورت زير تعريف مي گردد :

به طوريکه :

اگربخواهيم تابع بسل نوع دوم را در يک نقطه حساب کنيم دستور آن به صورت زير مي باشد :

>>K= besselk(v,x)

تابع بسل نوع سوم
اين نوع بسل مربوط به معادله زير مي باشد و به تابع Hankel نيزموسوم مي باشد :

در اين حالت تابع بسل به صورت زير تعريف مي گردد :

به طوريکه تابع bessely مي باشد .
رابطه اين دو نوع بسل به شکل زير مي باشد :

گربخواهيم اين نوع تابع بسل را در يک نقطه حساب کنيم دستور آن به صورت زير مي باشد :

>>H = besselh(v,x)
مي باشد.k=1که