
شبیه سازی سیستم های دینامیکی
در این بخش به بررسی مفهوم شبیه سازی سیستم های دینامیکی در ابزار سیمولینک نرم افزار متلب می پردازیم.
شبیه سازی سیستم های دینامیکی
امروزه کامپیوترها امکانات ریاضیاتی بسیار وسیعی را در اختیار مهندسین قرار می دهند، که می توان از آنها جهت شبیه سازی سیستم های دینامیکی استفاده نمود، که این مطلب باعث می شودی تا بدون نیاز به ایجاد و ساخت سیستم حقیقی، بتوان خواص و پاسخ آن را به تحریک هاک مختلف پیشگویی نمود. شبیه سازی سیستم های دینامیکی هنگام طراحی سیستم های کنترل بسیار مفید می باشد. زیرا موجب صرفه جویی در زمان و هزینه های مربوط به نمونه سازی سیستم فیزیکی مورد نظر خواهد شد.
جعبه ابزار سیمولیک در متلب
سیمولینک یک نرم افزار بسیار قدرتمند می باشد که به نرم افزار MATLAB ضمیمه شده و بصورت یکی از جعبه ابزارهای آن در آمده است. نرم افزار متلب با توجه به قابلیت تحلیل های عددی وسیعی که دارد، به نرم افزار قدرتمند در این زمینه بدل شده است.
جعبه ابزار سیمولینک ابزاری جهت شبیه سازی سیستم های دینامیکی (سیستم هایی که شامل چندین معادله دیفرانسیل حاکم بر سیستم می باشند.) و نمایش نتایج به صورت گرافیکی می باشد. هر حلقه منطقی، یا سیستم کنترلی، مربوط به سیستم های دینامیکی را می توان با استفاده از بلوک های آماده استاندارد موجود در کتابخانه سیمولینک، شبیه سازی نمود. مهمترین مزیت نرم افزار Simulink داشتن بلوک های آماده است، که نیاز به نوشتن برنامه را برای تحلیل های ریاضیاتی کوتاه از میان می برد.
آموزش محیط شبیه سازی سیمولینک متلب (Simulink) – قسمت هفتم – شبیه سازی حرکت یک پرتابه (Projectile) با سیمولینک متلب
در قسمت هفتم آموزش شبیه سازی در محیط سیمولینک متلب به شبیه سازی حرکت یک پرتابه می پردازیم. طرح شماتیک و معادلات حرکت یک پرتابه به صورت زیر بیان می گردد:
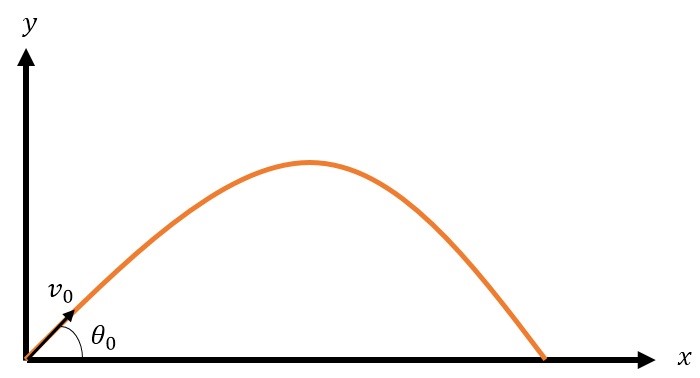

که در آن x0 , y0 موقعیت اولیه پرتابه می باشد که در این مثال چون مبدا مختصات روی پرتابه قرار دارد مقادیر آن ها صفر می باشد. v0 سرعت اولیه پرتابه و teta0 زاویه پرتاب می باشد که در این مثال فرضا v0=8 m/s و teta0=pi/4 در نظر می گیریم. همانطور که مشاهده می شود معادله حرکتی پرتابه در جهت x و y بر حسب زمان (t) بدست آمده اند. در آغاز معادله x را شبیه سازی می کنیم. سمت راست معادله سه پارامتر ثابت x0, v0 و teta0 داریم که می توانیم برای ایجاد آن ها از بلوک Constant استفاده کرده و برای ساخت t از بلوک clock استفاده می کنیم. در نهایت با توجه به آموزش های قسمت های پیشین و استفاده از بلوک های Sum و Product داریم:
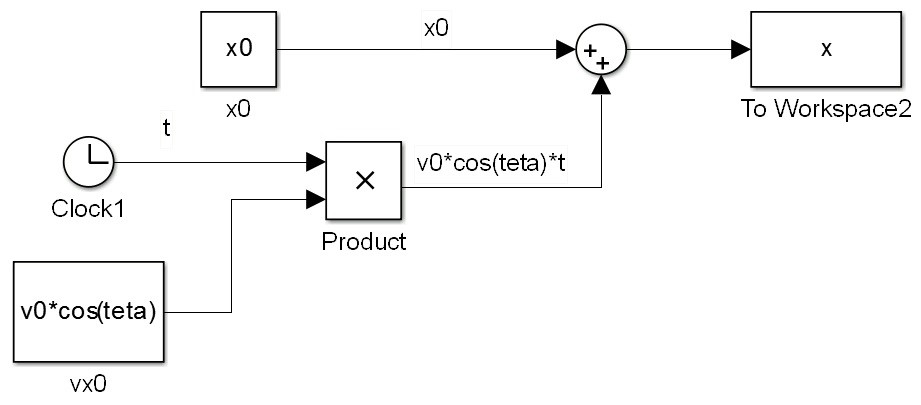
توجه کنید که تمامی مقادیر ثابت را بر خلاف قسمت های فبلی آموزش به صورت پارامتری وارد کرده ایم. برای مدلسازی متغیر y نیز به صورت زیر عمل می کنیم ( در این مدلسازی برای ایجاد تابع 0.5*(t^2) از بلوک fcn استفاده کرده ایم). داریم:
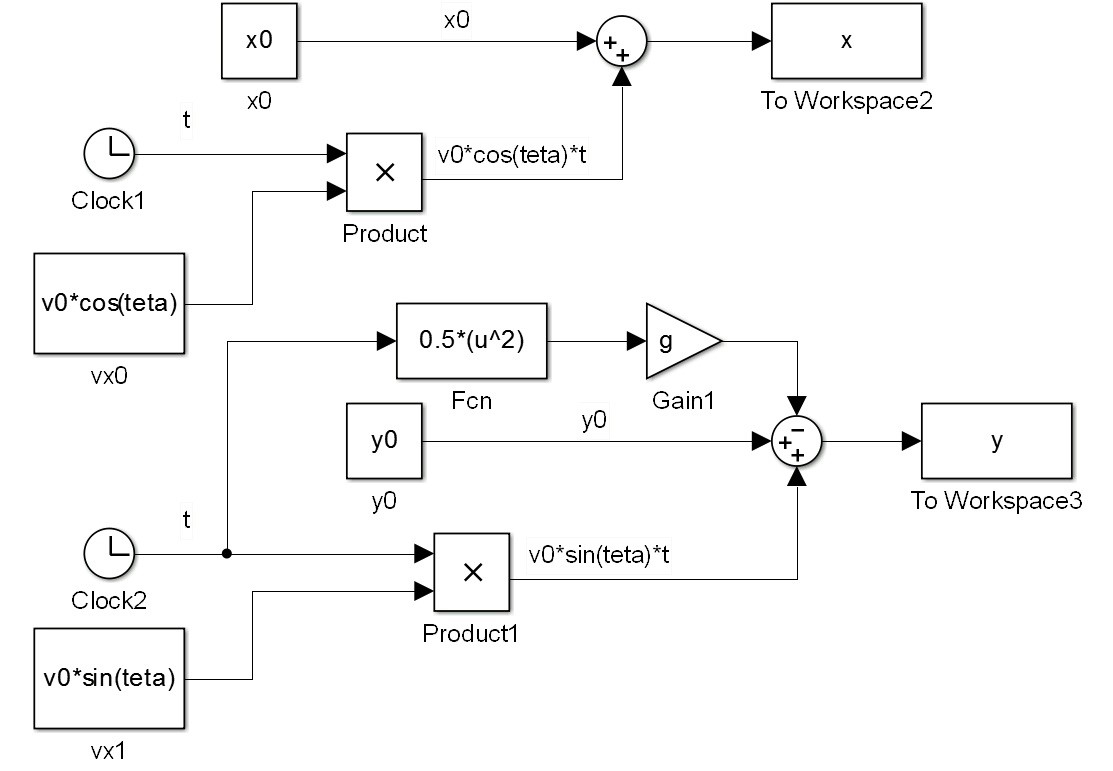
تا این مرحله متغیرهای x و y را مدلسازی کرده ایم. اما هنوز پارامترهای ثابت آن مانند x0, y0, teta0 , v0 و g را به محیط شبیه سازی معرفی نکرده ایم. (همه به صورت پارامتری تعریف شده اند). برای تعریف غیر مستقیم پارامترهای ثابت کافیست در صفحه اصلی شبیه سازی کلیک راست کرده و گزینه Model Properties را انتخاب کنید.

ار تب Callbacks پنجره InitFcn را انتخاب کرده (هر دستوری که در این پنجره وارد شود قبل از آغاز به کار برنامه، توسط محیط شبیه سازی از این قسمت پردازش می شود. برای مثال در این پنجره 5 پارامتر ثابت را معرفی می کنیم. داریم:
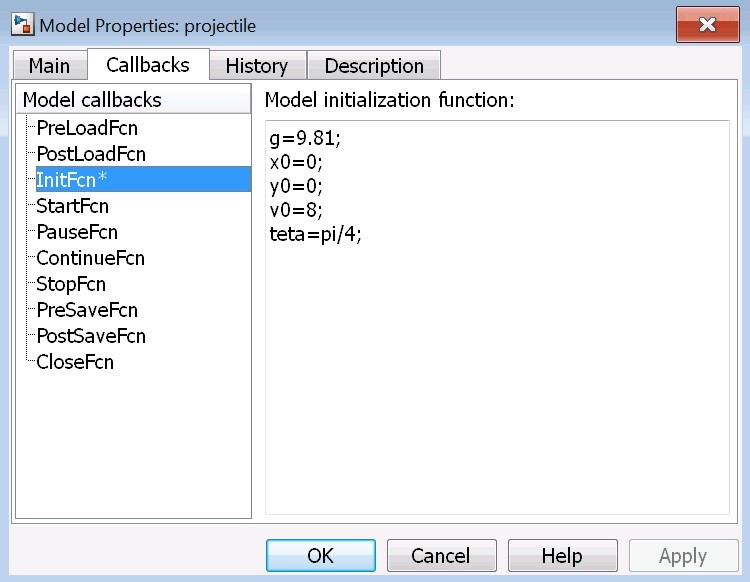
پس از این طریق پارامترهای سیستم را به طور غیر مستقیم وارد فاز محاسباتی می کنیم. هدف ما ترسیم y بر حسب x می باشد که می توانیم از دستور plot استفاده کنیم. می توان مجددا ار تب Callbacks پنجره StopFcn را انتخاب کرده و دستور plot را در این پنجره مطابق شکل زیر وارد کنیم تا پس از پایان شبیه سازی مسیر پرتابه ترسیم گردد.

در نهایت مسیر حرکت پرتابه به صورت زیر ترسیم می شود:
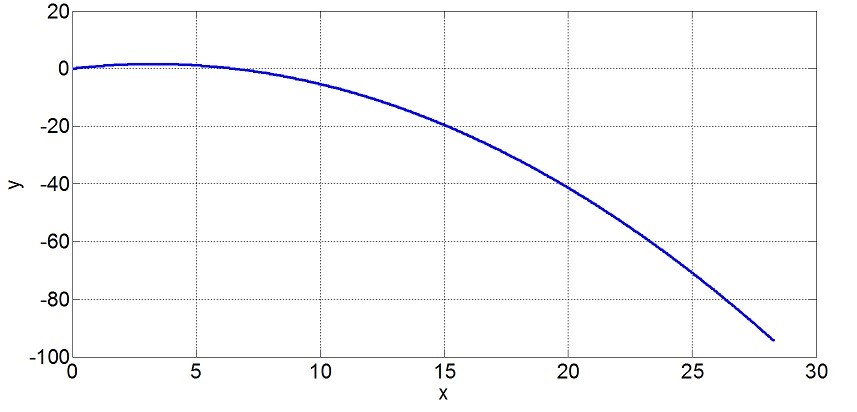
اما نمودار ترسیم شده آن چیزی نیست که ما انتظار داریم زیرا y<0 برای حرکت پرتابه به این خاطر بی معنی ست که پرتابه به علت سرعت اولیه و زاویه پرتاب ابتدا اوج می گیرد و نهایتا پرتابه در کمترین ارتفاع به زمین می خورد یعنی y=0 ، پس باید کاری کنیم که شبیه سازی در این حالت متوقف شود.
