این مطلب بررسی برنامه نوشته شده “مدیریت بهینه انرژی سیستم های نیروی هیبریدی بادی-باتری با برنامه نویسی دینامیک دودویی” است که کد ها را میتوانید در همین مطلب دانلود کنید.
بررسی برنامه نوشته شده:
فایل data4 :
شماره گذاری این فایل با 4 به این جهت است که با پروژه های قبلی و بعدی اشتباه نشود.
clear all; پاکسازی تمامی داده های قبلی و صفحه نمایش
clc;
n=7; مشخص نمودن تعداد ژنراتورها در این متغییر
alfa=[75.5 83.2 95.3 69.9 115 120 110.4]; , وارد نمودن ضرایب مربوط به تابع هزینه بر حسب توان
betta=[7.3 9.6 2.3 6.6 9.2 8.7 4.5];
gama=[152 163 198 147 123 369 870]*1e-8;
max_power=[300 500 350 360 480 430 390]; حداکثر توان تولید واحدها در این ماتریس داده می شود.
up_time=[1 0 0 2 1 0 1];محدودیتهای مربوط به زمان خاموش و روشن کردن واحدها
down_time=[1 0 2 3 0 0 2];
graph=[1400 1200 1100 1000 900 800 800 850 950 950 1000 1050 1100 1100 1150 1300 1400 1500 1800 1900 1800 1850 1600 1500 ]; رژیم مصرف بار شبکه در 24 ساعت یک شبانه روز
unite=zeros(24,7);
فایل body4 :
data4; در این قسمت داده ها فراخوانی میشوند
Power=zeros(24,7);
for h=1:24 برای 24 ساعت شبانه روز هر بار تمامی محاسبات زیر صورت می گیرد
n=7;
for i=1:n میانگین قیمت واحد ها به صورت گفته شده در مقدمه محاسبه می گردد
average(2,i)=(alfa(i)+betta(i)*max_power(i)+gama(i)*(max_power(i)^2))/max_power(i);
average(1,i)=i;
end
[sorted, num] = sort(average, 2);
تمامی واحدها بر حسب میانگین قیمتها مرتب می شوند ودر ضمن شماره تمامی آنها هم به حافظه سپرده می شود تا از اشتباه جلوگیری شود مثلا اگر واحد 3 کمترین مصرف را دارد به جای واحد 1 قرار نگیرد
تمامی مشخصات واحد ها در یک ماتریس به نام sorted گرد آوری می شود تا کار برنامه نویسی راحتتر شود.
for i=1:n
sorted(1,i)=num(2,i);
sorted(3,i)=max_power(num(2,i));
sorted(4,i)=up_time(num(2,i));
sorted(5,i)=down_time(num(2,i));
end
جمع توانهای واحد ها بر حسب لیست تقدم انجام می گیرد تا بتوان این جمع را با مصرف کل هر ساعت مقایسه نمود.
sorted(6,1)=sorted(3,1);
for i=2:n
sorted(6,i)=sorted(3,i)+sorted(6,i-1); این جمع در درایه 6 ام ماتریس مذبور جای میگیرد.
end
%*********************<=>***************
در این قسمت از برنامه مصرف کل شبکه با واحد ها مقایسه می شود تا معلوم شود کدامیک از واحد ها باید خاموش یا روشن باشند
for i=1:n
if graph(h)<= sorted(6,i)
a=zeros(1,n);b=zeros(1,n);c=zeros(1,n);p=zeros(1,n);
for o=1:i
unite(h,sorted(1,o))=1; اگر هر یک از واحد ها نیاز باشد که روشن شوند با نماد یک در ماتریس یونیت ذخیره می شوند
a(sorted(1,o))=alfa(sorted(1,o)); در این قسمت تغییراتی جهت استفاده پخش بار اقتصادی در نظر گرفته شده است.
b(sorted(1,o))=betta(sorted(1,o));
c(sorted(1,o))=gama(sorted(1,o));
pr=graph(h);
end
break
end
end
شروط زیر می تواند واحدهای دارای min up time را شناسایی نماید به این ترتیب که شرط اول می گوید واحد باید در این ساعت خاموش شود ولی در حالیکه در ساعت قبلی روشن بوده و شرط آخری وجود این محدودیت را چک میکند.
for i=1:n
if (h>2 && unite(h,i)==0 && unite((h-1),i)==1 && up_time(i)~=0) %
unite(h,i)=3; در این قسمت واحد دارای محدودیت را با عدد 3 شناسایی میکنیم
average(2,i)=inf; % با اینکار میزان تولید واحد دارای محدودیت روشن شدن بی نهایت فرض می شود تا در آخر لیست حق تقدم قرار میگیرد و انگار از لیست خارج می شود .
SAVE=max_power(i);
max_power(i)=inf;
[sorted, num] = sort(average, 2);دوباره بر حسب لیست حق تقدم مرتب می شوند البته بدون واحد دارای محدودیت
for k=1:n دوباره همگی مراحل فوق در جایگزینی در ماتریس سورت شده انجام می گیرد.
sorted(1,k)=num(2,k);
sorted(3,k)=max_power(num(2,k));
sorted(4,k)=up_time(num(2,k));
sorted(5,k)=down_time(num(2,k));
end
.
max_power(i)=SAVE;
sorted(6,1)=sorted(3,1);
for i=2:n
sorted(6,i)=sorted(3,i)+sorted(6,i-1);
end
for i=1:n
if graph(h)<= sorted(6,i)
for t=1:i
unite(h,sorted(1,t))=1;
end
break
end
end
end تمامی این مراحل برای محدودیت حداقل زمان خاموشی نیز به کاررفته است
if down_time(i)~=0
if h>3 && unite(h,i)==1 && unite((h-down_time(i)),i)==0 && unite((h-down_time(i)-1),i)==1 % condition of recognization of down time
unite(h,i)=4;
end
end
end
eco_dispatch; در این قسمت برنامه پخش بار اقتصادی برگرفته از پروژه اول فراخوانی می شود
Power(h,1:7)=p(1:7);
su(h)=sum(Power(h,:));
end
ج) فایل پخش بار اقتصادی eco_dispatch;
landa=[8 9];حدس اولیه لاندا
n=7;
for k=1:100
for j=1:2
for i=1:n
محاسبه توان هر واحد
delta(i)=(b(i)^2-4*(a(i)-landa(j))*c(i))^0.5;
if c(i)>0
p(i)=(-b(i)+delta(i))/(2*c(i)) ;
end
محاسبه خطای هر مرحله
error(j)=pr-sum(p);
end
end
محاسبه لاندای جدید و جایگذاری لاندای جدید به جای قبلی
m=(landa(2)-landa(1))/(error(2)-error(1));
landa(3)=m*(0-error(2))+landa(2);
landa(1)=landa(2);
landa(2)=landa(3);
if (abs(error(2))<0.00001*pr)
break
end
end
د) فایل result4:
body4; ابتدا فایل محاسباتی فراخوانی می گردد
clc;
for h=1:24
fprintf(‘\n——————————-Economic dispatching————————————\t ‘);
fprintf(‘\nTime\t\t MODE\t Power MW\t\t ‘);سر برگ نمایشگر چاپ می شود
fprintf(‘\n %2.0f \t ‘,h);
for u=1:n
fprintf(‘ \n unite(%2.0f):\t ‘,u);
if unite(h,u)==1 fprintf(‘ on\t\t%2.2f \t\t\n’,Power(h,u));اگر یونیت برابر 1 بود یعنی روشن است
else if unite(h,u)==0 fprintf(‘off \t\t%2.2f \n’,Power(h,u));
اگر یونیت برابر 0 بود یعنی خاموش
است
else if unite(h,u)==3 fprintf(‘Min UP Time\t%2.2f \n’,Power(h-1,u));
اگر یونیت برابر 3 بود یعنی محدودیت مینیمم آپ تایم فعال است
else if unite(h,u)==4 fprintf(‘Min DOWN Time\t%2.2f \n’,Power(h-1,u) ); اگر یونیت اگر یونیت برابر 3 بود یعنی محدودیت مینیمم دان تایم فعال است
end
end
end
end
fprintf(‘ \n \t\t\t_________________________ ‘);
fprintf(‘ \n \t\t\tTotal Power=%2.3f ‘,su(h));جمع کل توانهای واحدها نمایش داده می شود
fprintf(‘ \n
end
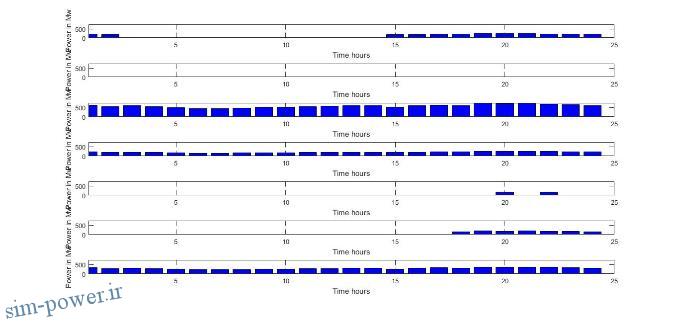
for j=1:n در این قسمت چند نمودار برای روشن شدن قضایا در نظر گرفته می شود.
for h=1:24
u=6*j-5;
name=[‘unite1’ ‘unite2’ ‘unite3’ ‘unite4’ ‘unite5’ ‘unite6’ ‘unite7’ ];
x(j,h)=Power(h,j);
y(h) =h;
X(1,h)=x(j,h);
end
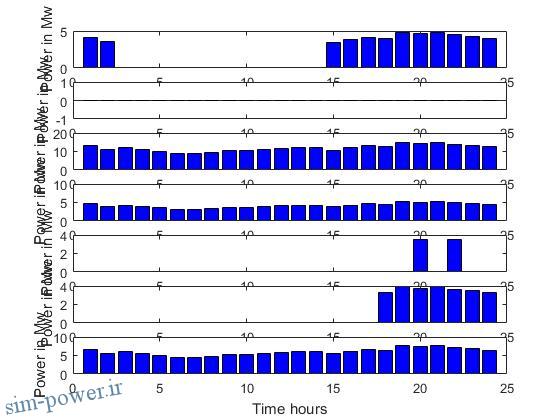
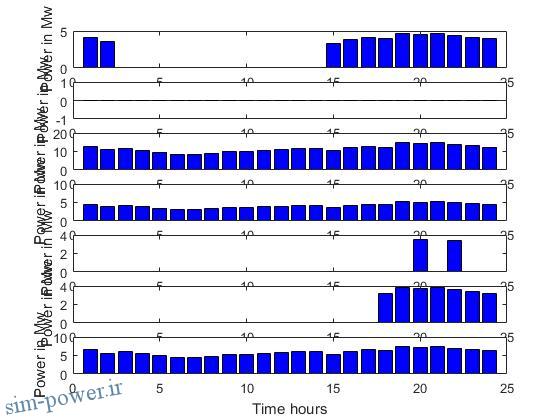
figure(1); bar(Power);ylabel(‘Power in Mw’);
xlabel(‘Time hours’); legend(‘unite1’, ‘unite2’, ‘unite3′ ,’unite4’ , ‘unite5’ , ‘unite6’ , ‘unite7’);axis([ 0 27 0 750]);
figure(2); stairs(Power);legend(‘unite1’, ‘unite2’, ‘unite3′ ,’unite4’ , ‘unite5’ , ‘unite6’ , ‘unite7′,’Location’,’NorthWest’);
figure(3);subplot(4,2,j);bar(X,’b’);axis([ 1 25 0 750]);
ylabel(‘Power in Mw’);
xlabel(‘Time hours’);
title(name(u:u+5));
end
هـ) نتایج و نمودارها :
پس ازاجرای فایل result4 این نتایج در ویندوز comment ظاهر می شود.

در ساعت اول نشان داده می شود که هریک از واحد ها چقدر باید تولید کنند و روشن یا خاموش بودن آنها بر حسب لیست حق تقدم نیز مشخص می گردد.

در ساعت سوم دستور خاموش شدن واحد 3 صادر می شود اما این واحد نمی تواند برای یک ساعت خاموش شود و باید در ساعت 4 خاموش گردد.
ابتدا می بایست توسط فایل data تمامی ورودی های مورد نیاز دریافت گردد.
clear all;
clc;
fprintf(‘ Saeed Arabameri \n\n Economical Dispaching \n\n\n’ );
func=input(‘Curve type or Line type?\nCrve=c \nline=l \n\n ‘, ‘s’ );
اگر برای ورودی func ورودی c لحاظ گردد برنامه کِرو اجرا می شود وگرنه برنامه تکه ای خطی اجرا خواهد شد
if func==’c’
n=7; تعداد واحدهای نیروگاهی در این قسمت معین می گردد
a=[7.2 7.3 7.85 7.91 7.4 7.98 7.25]; ماتریسهای آلفا بتا و گاما در این ناحیه تغییر داده شوند
b=[0.00142 0.00151 0.00194 0.00221 0.00162 0.00482 0.00148]; % B matrix
c=[10.1 11.2 12.7 7.11 16.8 5.2 3.1 ]*1e-6; % C matrix
pr=1400 ; % Total product in Mw
p_max=[600 300 400 300 400 200 600]; %Max power in Mw
p_min=[150 100 100 50 200 50 200 ]; %Min power in Mw
**********************************************************************
ابتدا به تشریح عملکرد برنامه چند جمله ای می پردازیم:
data;در اینجا فایل مشخصات صدا زده می شود
if func==’c’
for overshot=1:100 این حلقه برای محاسبه بالازدگی ماکزییمم توانهاست
for k=1:100 این حلقه برای محاسبه صرفا برای تکرار جهت کاهش خطاست
for j=1:2 این حلقه برای محاسبه دو عدد لاندا است تا بتوانیم روش تکرار لاندا را استفاده کنیم
for i=1:n این حلقه برای محاسبه هر تعداد واحد نیروگاهی است که در این مثال 7 است ولی میتواند هر عدد دیگری باشد
delta(i)=(b(i)^2-4*(a(i)-landa(j))*c(i))^0.5; در اینجا به محاسبه توان هر واحد نیروگاهی می پردازیم
if c(i)>0
p(i)=(-b(i)+delta(i))/(2*c(i)) ;
end
error(j)=pr-sum(p); خطای حاصله ا ز هر دفعه محاسبه حساب می شود
end
end
m=(landa(2)-landa(1))/(error(2)-error(1)); شیب حاصل از خطا ها و لاندهای 1 و 2 محاسبه می شود
landa(3)=m*(0-error(2))+landa(2); یک لاندا جدید محاسبه می شود که محل برخوردش با محور افقی است
landa(1)=landa(2); لاندا جدید در این قسمت جایگزین می شود
landa(2)=landa(3);
if (abs(error(2))<0.00001*pr) اگر در این مرحله خطا کمتر از حدی بود حلقه قطع می گردد
break
end
end
خروجی نمودارها:
مدیریت انرژی بهینه سیستم های نیروی هیبریدی بادی-باتری با برنامه نویسی دینامیک دودویی
بررسی برنامه نوشته شده:
فایل data4 :
شماره گذاری این فایل با 4 به این جهت است که با پروژه های قبلی و بعدی اشتباه نشود.
clear all; پاکسازی تمامی داده های قبلی و صفحه نمایش
clc;
n=7; مشخص نمودن تعداد ژنراتورها در این متغییر
alfa=[75.5 83.2 95.3 69.9 115 120 110.4]; , وارد نمودن ضرایب مربوط به تابع هزینه بر حسب توان
betta=[7.3 9.6 2.3 6.6 9.2 8.7 4.5];
gama=[152 163 198 147 123 369 870]*1e-8;
max_power=[300 500 350 360 480 430 390]; حداکثر توان تولید واحدها در این ماتریس داده می شود.
up_time=[1 0 0 2 1 0 1];محدودیتهای مربوط به زمان خاموش و روشن کردن واحدها
down_time=[1 0 2 3 0 0 2];
graph=[1400 1200 1100 1000 900 800 800 850 950 950 1000 1050 1100 1100 1150 1300 1400 1500 1800 1900 1800 1850 1600 1500 ]; رژیم مصرف بار شبکه در 24 ساعت یک شبانه روز
unite=zeros(24,7);
فایل body4 :
data4; در این قسمت داده ها فراخوانی میشوند
Power=zeros(24,7);
for h=1:24 برای 24 ساعت شبانه روز هر بار تمامی محاسبات زیر صورت می گیرد
n=7;
for i=1:n میانگین قیمت واحد ها به صورت گفته شده در مقدمه محاسبه می گردد
average(2,i)=(alfa(i)+betta(i)*max_power(i)+gama(i)*(max_power(i)^2))/max_power(i);
average(1,i)=i;
end
[sorted, num] = sort(average, 2);
تمامی واحدها بر حسب میانگین قیمتها مرتب می شوند ودر ضمن شماره تمامی آنها هم به حافظه سپرده می شود تا از اشتباه جلوگیری شود مثلا اگر واحد 3 کمترین مصرف را دارد به جای واحد 1 قرار نگیرد
تمامی مشخصات واحد ها در یک ماتریس به نام sorted گرد آوری می شود تا کار برنامه نویسی راحتتر شود.
for i=1:n
sorted(1,i)=num(2,i);
sorted(3,i)=max_power(num(2,i));
sorted(4,i)=up_time(num(2,i));
sorted(5,i)=down_time(num(2,i));
end
جمع توانهای واحد ها بر حسب لیست تقدم انجام می گیرد تا بتوان این جمع را با مصرف کل هر ساعت مقایسه نمود.
sorted(6,1)=sorted(3,1);
for i=2:n
sorted(6,i)=sorted(3,i)+sorted(6,i-1); این جمع در درایه 6 ام ماتریس مذبور جای میگیرد.
end
%*********************<=>***************
در این قسمت از برنامه مصرف کل شبکه با واحد ها مقایسه می شود تا معلوم شود کدامیک از واحد ها باید خاموش یا روشن باشند
for i=1:n
if graph(h)<= sorted(6,i)
a=zeros(1,n);b=zeros(1,n);c=zeros(1,n);p=zeros(1,n);
for o=1:i
unite(h,sorted(1,o))=1; اگر هر یک از واحد ها نیاز باشد که روشن شوند با نماد یک در ماتریس یونیت ذخیره می شوند
a(sorted(1,o))=alfa(sorted(1,o)); در این قسمت تغییراتی جهت استفاده پخش بار اقتصادی در نظر گرفته شده است.
b(sorted(1,o))=betta(sorted(1,o));
c(sorted(1,o))=gama(sorted(1,o));
pr=graph(h);
end
break
end
end
شروط زیر می تواند واحدهای دارای min up time را شناسایی نماید به این ترتیب که شرط اول می گوید واحد باید در این ساعت خاموش شود ولی در حالیکه در ساعت قبلی روشن بوده و شرط آخری وجود این محدودیت را چک میکند.
for i=1:n
if (h>2 && unite(h,i)==0 && unite((h-1),i)==1 && up_time(i)~=0) %
unite(h,i)=3; در این قسمت واحد دارای محدودیت را با عدد 3 شناسایی میکنیم
average(2,i)=inf; % با اینکار میزان تولید واحد دارای محدودیت روشن شدن بی نهایت فرض می شود تا در آخر لیست حق تقدم قرار میگیرد و انگار از لیست خارج می شود .
SAVE=max_power(i);
max_power(i)=inf;
[sorted, num] = sort(average, 2);دوباره بر حسب لیست حق تقدم مرتب می شوند البته بدون واحد دارای محدودیت
for k=1:n دوباره همگی مراحل فوق در جایگزینی در ماتریس سورت شده انجام می گیرد.
sorted(1,k)=num(2,k);
sorted(3,k)=max_power(num(2,k));
sorted(4,k)=up_time(num(2,k));
sorted(5,k)=down_time(num(2,k));
end
.
max_power(i)=SAVE;
sorted(6,1)=sorted(3,1);
for i=2:n
sorted(6,i)=sorted(3,i)+sorted(6,i-1);
end
for i=1:n
if graph(h)<= sorted(6,i)
for t=1:i
unite(h,sorted(1,t))=1;
end
break
end
end
end تمامی این مراحل برای محدودیت حداقل زمان خاموشی نیز به کاررفته است
if down_time(i)~=0
if h>3 && unite(h,i)==1 && unite((h-down_time(i)),i)==0 && unite((h-down_time(i)-1),i)==1 % condition of recognization of down time
unite(h,i)=4;
end
end
end
eco_dispatch; در این قسمت برنامه پخش بار اقتصادی برگرفته از پروژه اول فراخوانی می شود
Power(h,1:7)=p(1:7);
su(h)=sum(Power(h,:));
end
ج) فایل پخش بار اقتصادی eco_dispatch;
landa=[8 9];حدس اولیه لاندا
n=7;
for k=1:100
for j=1:2
for i=1:n
محاسبه توان هر واحد
delta(i)=(b(i)^2-4*(a(i)-landa(j))*c(i))^0.5;
if c(i)>0
p(i)=(-b(i)+delta(i))/(2*c(i)) ;
end
محاسبه خطای هر مرحله
error(j)=pr-sum(p);
end
end
محاسبه لاندای جدید و جایگذاری لاندای جدید به جای قبلی
m=(landa(2)-landa(1))/(error(2)-error(1));
landa(3)=m*(0-error(2))+landa(2);
landa(1)=landa(2);
landa(2)=landa(3);
if (abs(error(2))<0.00001*pr)
break
end
end
د) فایل result4:
body4; ابتدا فایل محاسباتی فراخوانی می گردد
clc;
for h=1:24
fprintf(‘\n——————————-Economic dispatching————————————\t ‘);
fprintf(‘\nTime\t\t MODE\t Power MW\t\t ‘);سر برگ نمایشگر چاپ می شود
fprintf(‘\n %2.0f \t ‘,h);
for u=1:n
fprintf(‘ \n unite(%2.0f):\t ‘,u);
if unite(h,u)==1 fprintf(‘ on\t\t%2.2f \t\t\n’,Power(h,u));اگر یونیت برابر 1 بود یعنی روشن است
else if unite(h,u)==0 fprintf(‘off \t\t%2.2f \n’,Power(h,u));
اگر یونیت برابر 0 بود یعنی خاموش
است
else if unite(h,u)==3 fprintf(‘Min UP Time\t%2.2f \n’,Power(h-1,u));
اگر یونیت برابر 3 بود یعنی محدودیت مینیمم آپ تایم فعال است
else if unite(h,u)==4 fprintf(‘Min DOWN Time\t%2.2f \n’,Power(h-1,u) ); اگر یونیت اگر یونیت برابر 3 بود یعنی محدودیت مینیمم دان تایم فعال است
end
end
end
end
fprintf(‘ \n \t\t\t_________________________ ‘);
fprintf(‘ \n \t\t\tTotal Power=%2.3f ‘,su(h));جمع کل توانهای واحدها نمایش داده می شود
fprintf(‘ \n
end
for j=1:n در این قسمت چند نمودار برای روشن شدن قضایا در نظر گرفته می شود.
for h=1:24
u=6*j-5;
name=[‘unite1’ ‘unite2’ ‘unite3’ ‘unite4’ ‘unite5’ ‘unite6’ ‘unite7’ ];
x(j,h)=Power(h,j);
y(h) =h;
X(1,h)=x(j,h);
end
figure(1); bar(Power);ylabel(‘Power in Mw’);
xlabel(‘Time hours’); legend(‘unite1’, ‘unite2’, ‘unite3′ ,’unite4’ , ‘unite5’ , ‘unite6’ , ‘unite7’);axis([ 0 27 0 750]);
figure(2); stairs(Power);legend(‘unite1’, ‘unite2’, ‘unite3′ ,’unite4’ , ‘unite5’ , ‘unite6’ , ‘unite7′,’Location’,’NorthWest’);
figure(3);subplot(4,2,j);bar(X,’b’);axis([ 1 25 0 750]);
ylabel(‘Power in Mw’);
xlabel(‘Time hours’);
title(name(u:u+5));
end
هـ) نتایج و نمودارها :
پس ازاجرای فایل result4 این نتایج در ویندوز comment ظاهر می شود.
در ساعت اول نشان داده می شود که هریک از واحد ها چقدر باید تولید کنند و روشن یا خاموش بودن آنها بر حسب لیست حق تقدم نیز مشخص می گردد.

در ساعت سوم دستور خاموش شدن واحد 3 صادر می شود اما این واحد نمی تواند برای یک ساعت خاموش شود و باید در ساعت 4 خاموش گردد.
ابتدا می بایست توسط فایل data تمامی ورودی های مورد نیاز دریافت گردد.
clear all;
clc;
fprintf(‘ Saeed Arabameri \n\n Economical Dispaching \n\n\n’ );
func=input(‘Curve type or Line type?\nCrve=c \nline=l \n\n ‘, ‘s’ );
اگر برای ورودی func ورودی c لحاظ گردد برنامه کِرو اجرا می شود وگرنه برنامه تکه ای خطی اجرا خواهد شد
if func==’c’
n=7; تعداد واحدهای نیروگاهی در این قسمت معین می گردد
a=[7.2 7.3 7.85 7.91 7.4 7.98 7.25]; ماتریسهای آلفا بتا و گاما در این ناحیه تغییر داده شوند
b=[0.00142 0.00151 0.00194 0.00221 0.00162 0.00482 0.00148]; % B matrix
c=[10.1 11.2 12.7 7.11 16.8 5.2 3.1 ]*1e-6; % C matrix
pr=1400 ; % Total product in Mw
p_max=[600 300 400 300 400 200 600]; %Max power in Mw
p_min=[150 100 100 50 200 50 200 ]; %Min power in Mw
**********************************************************************
ابتدا به تشریح عملکرد برنامه چند جمله ای می پردازیم:
data;در اینجا فایل مشخصات صدا زده می شود
if func==’c’
for overshot=1:100 این حلقه برای محاسبه بالازدگی ماکزییمم توانهاست
for k=1:100 این حلقه برای محاسبه صرفا برای تکرار جهت کاهش خطاست
for j=1:2 این حلقه برای محاسبه دو عدد لاندا است تا بتوانیم روش تکرار لاندا را استفاده کنیم
for i=1:n این حلقه برای محاسبه هر تعداد واحد نیروگاهی است که در این مثال 7 است ولی میتواند هر عدد دیگری باشد
delta(i)=(b(i)^2-4*(a(i)-landa(j))*c(i))^0.5; در اینجا به محاسبه توان هر واحد نیروگاهی می پردازیم
if c(i)>0
p(i)=(-b(i)+delta(i))/(2*c(i)) ;
end
error(j)=pr-sum(p); خطای حاصله ا ز هر دفعه محاسبه حساب می شود
end
end
m=(landa(2)-landa(1))/(error(2)-error(1)); شیب حاصل از خطا ها و لاندهای 1 و 2 محاسبه می شود
landa(3)=m*(0-error(2))+landa(2); یک لاندا جدید محاسبه می شود که محل برخوردش با محور افقی است
landa(1)=landa(2); لاندا جدید در این قسمت جایگزین می شود
landa(2)=landa(3);
if (abs(error(2))<0.00001*pr) اگر در این مرحله خطا کمتر از حدی بود حلقه قطع می گردد
break
end
end
خروجی نمودارها: