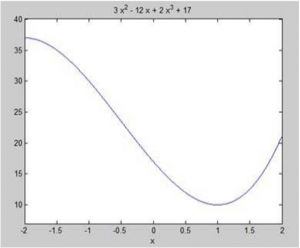
پیدا کردن حداقل و حداکثر از منحنی
اگر ما حداقل و حداکثر را از یک نمودار جستجو کنیم، ما به ط.ر اساسی بیش ترین و کمترین نقاط روی نمودار از یک تابع در محل خاص یا محدوده خاصی از مقادیر از متغیر نمادین را جستجو می کنیم.
برای تابع y=f(x) نقاط روی نمودار که در نمودار شیب صفر دارند نقاط ایستا نامیده می شوند. به عبارت دیگر نقاط ایستا f’(x)=0 هستند.
برای پیدا کردن نقاط ایستا از تابع دیفرانسیل ما ، نیاز به مجموعه مشتق معادله صفر و حل معادلات داریم.
مثال
اجازه دهید نقاط ایستا از تابع f(x)=2x3+3x2-12x+17 را در مراحل زیر بگیریم:
1.اول اجازه دهید تابع را وارد کنیم و نمودار آن را رسم کنیم:
syms x
y =2*x^3+3*x^2-l2*x +17;% defining the function
ezplot(y)
متلب کد را اجرا می کند و طرح زیر را برمی گرداند:
اینجا کد معادل octave برای مثال بالا است:
pkg load symbolic
symbols
x = sym )‘ x'( :
y =inline(“2*x^3 + 3*x^2 – l2*x + l7”);
ezplot(y)
print-deps gxaph.eps
- فرض ما بر این است که تعدادی محل حداکثر و حداقل روی نمودار وجود دارد، بنابراین ما محل حداکثر و حداقل برای فاصله زمانی[-2,2] را بر روی نمودارنشان می دهیم.
syms x
y =2*x^3+3*x^2-l2*x +17;% defining the function
ezplot (y, [-2, 2])
متلب کد را اجرا خواهد کرد و طرح زیر را بر می گرداند:
اینجا کد معادل octave برای مثال بالا است:
pkg load symbolic
symbols
x = sym )‘ x’);
y =inline(“2*x^3 + 3*x^2 – l2*x + l7”);
ezplot (y, [-2, 2l)
print-deps gxaph.eps
q = diff(y)
بعد ، اجازه دهید مشتق را محاسبه کنیم
متلب کد را اجرا می کند و نتایج زیر را بر می گرداند:
اینجا معادل octave محاسبات بالا است::
pkg load symbolic
symbols
x = ( ii xii) ;
y =2*xa3+3*xa2-l2*x +17;
g = differentiate(y,x)
4. let us solve the derivative function, g, to get the values where it becomes zero.
s = solve(g)
متلب کد را اجرا خواهد کرد و نتیجه زیر را برمی گرداند:
در زیر معادلoctave از محاسبات بالا است:
pkg load symbolic
symbols
x =sym(“x”) ;
y =2*x^3+3*x^2-12*x +17;
g = differentiate(y,x)
roots([6,6,-12])
subs(y,1), subs(y,-2)
این با طرح ما موافق است.بنابراین اجازه دهید تابع f در نقاط بحرانی x=1,-2 را ارزیابی کنیم. ما می توانیم مقدار در تابع نمادین را با استفاده از دستورsubs تعویض کنیم.
متلب کد را اجرا خواهد کرد و نتیجه زیر را بازمی گرداند:
معادل octaveاز محاسبات بالا در زیر آمده است:
pkg load symbolic
symbols
x = sym(“x”) ;
y =2*x^3+3*x^2-12*x +17;
g = differentiate(y,x)
roots([6,6,-12])
subs(y, x,1), subs(y, x,-2)
اغلب مقادیر حداقل و حداکثر بر روی تابع f(x)=2x3+3x2-12x+17، در فاصله زمانی [-2,2] 10و 37 هستند.
نویسنده: مهندس عربعامری
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,