گام بیست وچهارم: ادغام در متلب
ادغام با دو نوع از مسائل اساساً مختلف سر و کار دارد.
- در نوع اول، مشتق تابع داده شده و ما می خواهیم تابع را به دست بیاوریم. بنابراین، اساساً معکوس روند مشتق گیری است. روند معکوس به عنوان ضد مشتق گیری شناخته می شوند، یا تابع اولیه یا انتگرال معین پیدا می کنند.
- نوع دوم از مسائل شامل اضافه کردن تعداد زیادی از مقادیر بسیار کم و سپس حد گرفتن از اندازه مقادیر نزدیک به صفر، در حالی که تعدادی از شرایط گرایش به بی نهایت دارند. این روند منجر به تعریف انتگرال معین می شود.
انتگرال معین برای پیداکردن مساحت ، حجم، مرکز ثقل، لحظه جبری، کار انجام شده با نیرو، و در برنامه های کاربردی متعدد دیگر استفاده می شود.
پیداکردن انتگرال نامعین در متلب
به این معنی که، اگر مشتق تابع f(x)f’(x) است ، در آن صورت ما می گوییم انتگرال نامعین از f’(x) به x از f(x) گرایش دارد.برای مثال، از مشتق( با گرایش به x) از x2، 2x است، ما می توانیم بگوییم انتگرال نامعین از 2x، x2 است.
در نشانه ها:
f’(x2)=2x، بنابراین،
2xdx=x2ʃ
انتگرال نامعین منحصر به فرد نیست، زیرا مشتق ازx2+c، برای هر مقدار از ثابتc، نیز 2x خواهد بود.
این نماد به این صورت بیان شده است:
ʃ2xdx=x2+c.
که ،c‘ثابت اختیاری’ نامیده می شود.
متلب دستور int را برای محاسبه انتگرال از عبارت فراهم می کند. برای مشتق گیری عبارت برای انتگرال نامعین از تابع می نویسیم:
برای مثال، از مثال قبلی ما:
|
symsx int(2 * x) |
متلب دستور بالا را اجرا خواهد کرد و نتیجه زیر را بر می گرداند:
مثال 1
در این مثال، اجازه دهید انتگرال از تعدادی عبارت استفاده شده به طور معمولی را پیدا کنیم. یک فایل اسکریپت ایجاد نمایید و کد زیر را در آن تایپ نمایید
|
symsxn int(sym(x^n)) f =‘sin(n*t)‘ int(sym(f)) symsat int(a*cos(pi*t)) int(a^x) |
زمانی که شما فایل را ایجاد می کنید،نتیجه زیر نشان داده می شوند.
مثال 2
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
|
symsxn int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pxetty(int(1-10*x +9* x^2)) int((3+5*x -6*x^2-7*x^3)/2*x^2) pretty(int((3+5*x -6*x^2-7*x^3)/2*x^2)) |
توجه کنید که دستورpretty عبارت را بیشتر در قالب خواندنی برمی گرداند.
زمانی که فایل را اجرا می کنید، نتیجه زیر نشان داده می شود:
جستجوی انتگرال معین برای استفاده در متلب
به این مفهوم که، انتگرال معین ا ساساً حدی از جمع است، ما انتگرال معین را برای پیدا کردن مناطقی مانند مناطق بین منحنی و محور x و منطقه بین دو منحنی استفاده می کنیم. انتگرال معین همچنین می تواند در دیگر محل ها مورد استفاده قرار گیرد، که مقادیر مورد نیاز می تواند به عنوان حدی از جمع بیان شود.
دستور int می تواند برای ادغام عبور حدها بر روی انتگرالی که شما می خواهید محاسبه کنیداستفاه شود.
برای محاسبه
می نویسیم،
برای مثال، برای محاسبه می نویسیم:
int(x,4,9)
متلب دستورات بالا را اجرا خواهد کرد و نتیجه زیر را بازمی گرداند:
در زیر معادله octave محاسبات بالا است:
pkg load symbolic
symbols
x = sym(“x”):
f = x;
c = [1, 0] :
integral = polyint(c);
a = polyval(integral,9)- polyval(integral,4);
display(‘area: ‘), disp(double(a));
راه حل متناوب می تواند با استفاده از تابعquad()داده شده به صورت زیر فراهم شود:
pkg load symbolic
symbols
f =inline(“x”);
[a, ierror, nfneval]= quad(f,4,9);
display(‘area: ‘), disp(double(a));
مثال1
اجازه دهید محل در میان قرار گرفته شده در بین محورxو منحنیy=x3-2x+5 و عرض x=1و x=2 را محاسبه نماییم.
محل مورد نیاز به این صورت داده شده است:
یک فایل اسکریپت ایجاد کنید و کد زیر را تایپ نمایید:
f = x^3-2*x +5;
a =int (f, 1, 2)
display(‘area: ‘), disp(double(a));
زمانی که شما فایل را ایجاد می کنید، نتیجه زیر نمایش می یابد:
معادلهoctaveمحاسبات بالا در زیر آمده است:
pkg load symbolic
symbols
x = sym(“x”):
f = x^3-2*x +5;
c =[l,0,-2, 5]
integral = polyint(c);
a = polyval(integral,2)- polyval(integral,l);
display(‘area: ‘), disp(double(a));
راه حل متناوب می تواند با استفاده از تابع quad() داده شده octaveزیر را فراهم کند:
pkg load symbolic
symbols
x = ( “x” ) ;
f =inline(“x^3 – 2*x +5”);
[a, ierror, nfneval]= quad(f,l,2);
display(‘area: ‘), disp(double(a));
مثال 2
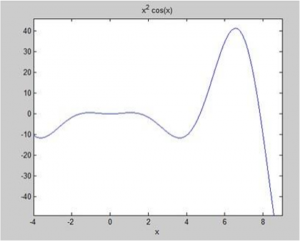
ناحیه زیر منحنی پیدا می شود:f(x)=x2cos(x)for-4 .
یک فایل اسکریپت ایجاد کنید و کد زیر را تایپ نمایید:
f = x^2*cos(x);
ezplot(f,[-4,9])
a =int(f,-4,9)
disp(‘axea: ‘), disp(double(a));
زمانی که فایل را اجرا می کنید، متلب نمودار را رسم می کند:
و نتایج زیر نشان داده می شود:
a
8*cos(4) + l8*cos(9) + l4*sin(4) + 79*sin(9)
area:
0.3326
در زیر معادله octave محاسبات بالا است:
pkg load symbolic
symbols
x = sym(“x”);
f =inline(“x^2*cos(x)”);
ezplot(f,[—4,9])
print-deps gxaph.eps
[a, ierror, nfneval]= quad(f,-4,9);
display(‘area: ‘), disp(double(a));
خرید کتاب 28 گام موثر در فتح متلب