اگر از اینرسی چرخ صرف نظر کنیم در اینصورت sys به جرم و دمپر تبدیل میشود
Y(s)/U(s)=1/(1000s+50)
Y(s)=سرعت
U(s)=نیرو
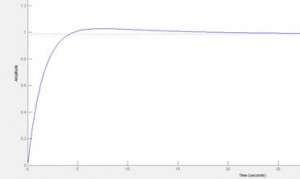
پاسخ حلقه باز به ورودی پله
ای(نیروی برابر 500نیوتن)
کنترل کننده PID با شرایط
1)وقتی نیروی موتور
500نیوتن حداکثر سرعت باید برابر 10 متر بر ثانیه باشد
2)زمان خیز باید کمتر از
5ثانیه باشد(risetime)
3)جهش کمتر از 10درصد
خطای حدود 2درصد در حالت ماندگار قابل
قبول است
مطلوبست:
بدست آوردن صفر و قطب های حلقه باز
بدست آوردن صفر و قطب های حلقه بسته در
حضور کنترل کننده PID
رسم مکان هندسی ریشه ها
رسم دیاگرام نایکوییست
حل:
ابتدا کد زیر را در متلب وارد
می کنیم:
clear all;
clc;
num=[1];
den=[1000
50];
g=tf(num,den);
[z,p,k]=tf2zp(num,den);
sisotool(g)
این کد
می تواند صفرها و قطبهای تابع حلقه باز را نمایش دهد:
z =
Empty matrix: 0-by-1
p =
-0.0500
k =
1.0000e-003
همانطور که در
جواب فوق دیده می شود صفر نداریم و تنها یک قطب در -0.0500
داریم و نیز بهره برابر 1.0000e-003 است.
حالا برای
یافتن صفر و قطبهای کنترلر مان از ابزار SISOTOOL کمک می گیریم:
یک عدد قطب
و یک صفر انتخاب می کنیم و آنقدر آنها را جابجا می
کنیم تا تمامی خواسته های مسئله برآورده گردد:
همانطور که در شکل می
بینید زمان نشست کمتر از 5 ثانیه شده است.
یکی
دیگر از خواسته های مسئله اورشوت است که باید زیر ده درصد
باشد این امر هم محقق شده است:
سیستم
زیر نمایش دهنده سیستم مورد دلخواه ماست که کنترلر PID آن یک قطب در 56 ویک
صفر در 8.8 داردو گین آن 4432 است
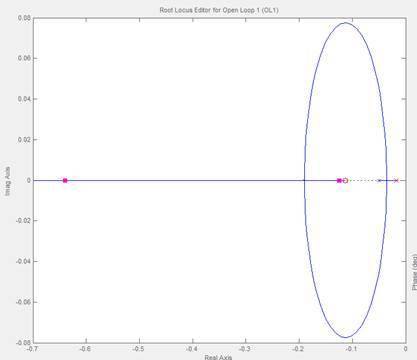
نمودار مکان هندسی این
سیستم این گونه می شود:
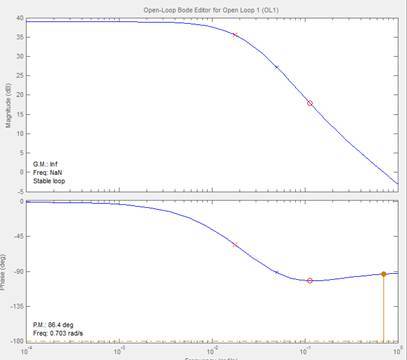
دیاگرام بود این سیستم نشان از
پایداری سیستم دارد:
همانطور که می بینید گین
مارجین و فیز مارجین هر دو در حدود خود قرار گرفته اند
وسیستم پایدار است البته این امر را می توانستیم
پیش بینی کنیم چون هیچ صفر و قطبی در سمت
راست محور کار نگذاشته ایم
دیاگرام نایکویست این سیستم
به شرح زیر است:
صفر و قطب تابع حلقه بسته:
برای اینکار هم از کدهای زیر
استفاده نمودیم:
clear all;
clc;
num=[1];
den=[1000
50];
g=tf(num,den);
[z,p,k]=tf2zp(num,den);
[num2,den2]=zp2tf(-1/8.8,-1/56,4432);
[numf,denf]=feedback(num,den,num2,den2);
F=tf(numf,denf)
[z2,p2,k2]=tf2zp(numf,denf)
که جواب به صورت زیر شده است:
Transfer function:
s + 0.01786
————————-
1000 s^2 + 4500 s + 504.5
z2 =
-0.0179
p2 =
-4.3848
-0.1151
k2 =
1.0000e-003