گام بیست و دوم: حساب دیفرانسیل و انتگرال در متلب

متلب روش های متفاوتی برای حل مسائل از محاسبات دیفرانسیل و انتگرال است، معادلات حل دیفرانسیل از هر مرتبه و محاسبه حدها .بهتر از همه، شما به راحتی می توانید نمودارهایی از توابع پیچیده و بررسی حداکثر، حداقل رسم نمایید و با دیگر نقاط نوشت افزار بر روی نمودار تابع اصلی را حل کنید، و همچنین از آن مشتق بگیرید.

در این فصل و چند فصل آینده، ما با مسائلی از محاسبات انتگرال و دیفرانسیل سر و کار خواهیم داشت. در این فصل ما درباره مفاهیم پیش از محاسبه انتگرال و دیفرانسیل بحث خواهیم کرد، به عنوان مثال، محاسبه حد توابع و بررسی خواص محدودیت.

در دیفرانسیل فصل بعد ما از عبارات مشتق می گیریم و محل حداکثر و حداقل را بر روی نمودار پیدا می کنیم. همچنین درباره حل معادلات دیفرانسیل بحث می کنیم.در نهایت، در فصل ادغام ما درباره محاسبه انتگرال بحث خواهیم کرد.

محاسبه انتگرال و دیفرانسیل حدها

متلب دستور limit را برای محاسبه حدها فراهم کرده است. در ساده ترین شکل آن، دستور limit عبارت را به صورت آرگومان می گیرد و حد عبارت را مستقل از متغیر صفر پیدا می کند.

برای مثال، اجازه دهید حد تابع³+5)/(x⁴+7) f(x)=(x را محاسبه کنیم. x به صفر میل می کند.

syms x

limit ( (x^3+5) / (x^4+7))

متلب دستورات بالا را اجرا خواهد کرد و نتیجه زیر را نشان می دهد:

دستور limit در حوزه ی محاسبات نمادین رخ می دهد؛ شما با استفاده از دستور syms به متلب می گویید که از متغیرهای نمادین استفاده کرده اید. شما همچنین می توانید حد توابع را ، به عنوان گرایش تعدادی دیگر از متغیرها به صفر محاسبه کنید. برای محاسبه lim_x->a(f(x))، ما از دستور limit با آرگومان هایش استفاده می کنیم.. اول بودن عبارت و دوم تعداد است، که نزدیک شدن x در اینجا به سمت a است.

برای مثال، به عنوان مثال اجازه دهید حد توابع f(x)=(x-3)/(x-1) را محاسبه کنیم، که x به سمت 1 میل می کند.

limit ( (x -3)/ (x-1) , 1)

متلب دستورات بالا را اجرا خواهد کرد و نتایج زیر را برمی گرداند:

اجازه دهید مثال دیگری بزنیم:

limit(x^2+5,3)

متلب دستور بالا را اجرا خواهد کرد ونتیجه زیر را نشان می دهد:

محاسبه حدها با استفاده از octave

در زیر نسخه octave از مثال بالا با استفاده از بسته نمادین است، سعی کنید نتایج را اجرا و محاسبه کنید:

pkg load symbolic

symbols

x=sym(“x”);

subs((x^3+5)/(x^4+7),x,0)

octave دستورات بالا را اجرا می کند و نتایج زیر را برمی گرداند:

تایید مشخصات اساسی حدها

قضیه حد اساسی تعدادی از مشخصات اساسی حدها را فراهم می آورد. به شرح زیر است:

اجازه دهید دو تابع زیر را در نظر بگیریم:

f(x)=(3x+5)/(x-3)
g(x)=x²+1.

اجازه دهید حدهایی از تابع x که به سمت 5 میل می کند، از هر دو تابع و خواص اولیه از حدها با استفاده از دو تابع در متلب بررسی می شود.

مثال

یک فایل اسکربیپت ایجاد کنید و کد زیر را در آن تایپ نمایید:

syms x

f =(3*x +5)/(x-3);

g = x^2+l;

11 = 1imit(f,4)

l2 = limit (g,4)

ladd = limit(f + g,4)

lsub = limit(f – g,4)

lmult = limit(f*q,4)

ldiv = limit (f/9,4)

زمانی که شما فایل را اجرا می کنید، این نمایش می یابد:

تایید مشخصات اساسی حدها با استفاده از octave

در زیر نسخه octave مثال بالا با استفاده از بسته symbolic است، سعی کنید نتایج را اجرا کنید:

pkg load symbolic

symbols

x = sym(“x”);

f =(3*x +5)/(x-3);

g = x^2+1;

l1=subs(f, x,4)

l2 = subs (g, x,4)

1add = subs (f+g, x,4)

lsub = subs (f-g, x,4)

lmult = subs (f*g, x,4)

ldiv = subs (f/g, x,4)

octave عبارات بالا را اجرا خواهد شد و نتایج زیر نشان داده می شود:

حد چپ و راست در متلب

زمانی که تابع برای تعداد خاص مقادیری از متغیرها ناپیوستگی دارند، حد در آن نقطه وجود ندارد. به عبارت دیگر، حدهایی از تابع f(x) در x=a ناپیوستگی دارد، زمانی که مقادیر حد، به عنوان x از سمت چپ به a نزدیک می شود، مقادیر حد از سمت راست به x نزدیک نمی شود.

این حد منجر به مفهوم حدهای سمت چپ و سمت راست می شود.حد سمت چپ به صورت x->a تعریف شد .a از سمت راست به صورت حدx->a ، از سمت راست ، به عنوان مثال x به a نزدیک می شود، برای مقادیر x>a است. تا زمانی که حد سمت چپ و حد سمت راست برابر نیستند، حد وجود ندارد.

اجازه دهید تابع را در نظر بگیریم:

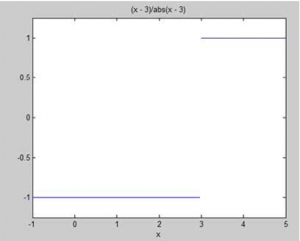
f(x)=(x-3)/|x-3|

ما نشان خواهیم داد کهlim_x->3f(x) وجود ندارد. متلب کمک می کند دو روش حقیقی را برقرار می کند: