گام بیست و هفتم: آشنایی با octave gnu
octave gnu یک زبان برنامه نویسی سطح بالا مانند متلب است و با متلب بسیار همساز است.همچنین برای محاسبات عددی استفاده می شود.
octave ویژگی های مشترکی با متلب دارد:
- ماتریس ها انواع داده بنیادی هستند
- ساختمان آن اعداد پیچیده را پشتیبانی می کند
- توابع تعریف شده – کاربر را پشتیبانی می کند
- octave gnu همچنین نرم افزار توزیع مجدد آزادانه است.شما ممکن است توزیع مجدد و یا را تحت واژه هایی از دانش عمومی کلی(gpl) به عنوان تاسیس نرم افزار رایگان انتشار نمایید.
octave در مقابل متلب
اکثر برناه های متلب در octave اجرا می شوند، اما برخی از برنامه های octave ممکن نیست که در متلب اجرا شوند زیرا، octave مجوز برخی نحوه اجرا در متلبمتلب را ندارند.
برای مثال، متلب تنها تک کوتیشن را پشتیبانی می کند، در حالی که متلب هر دو تک کوتیشن و جفت کوتیشن را برای رشته های معین پشتیبانی می کند. اگر شما در جستجو برای آموزش octave هستید، در آن صورت این آموزش دلپذیر از ابتدا هر دو متلب و همچنین octave را پوشش می دهد.
مثال های سازگار
تقریباً تمامی مثال ها در این آموزش سازگار با متلب همچنین octave هستند.اجازه دهید مثال زیر را در متلب و octave انجام دهیم که بدون تغییرات نحوه اجرا در متلبنتایج یکسانی را تولید می کند:
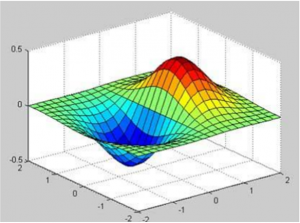
این مثال یک طرح 3d-max برای تابع g=xe-(x2*y2) ایجاد می کند. یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
[x, y] = meshgrid (-2: .2:2);
g = x .* exp(-x.^2- y.^2);
surf (x, y, g(
print:-deps graph . eps
زمانی که فایل را اجرا می کنید، متلب طرح سه بعدی زیر را نشان می دهد:
اگر چه تمام قابلیت های اصلی از متلب در دسترس octave است، برای مثال برخی دستورات محاسبه دیفرانسیل و انتگرال وجود دارند، که در هر دو زبان دقیقاً منطبق نیستند. این آموزش سعی دارد هر دو نوع از مثال را با تفاوت در نحوه اجرا در متلبآن ها بدهد.
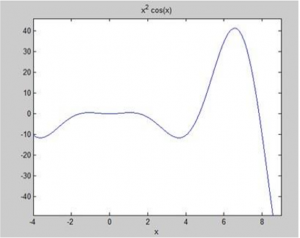
مثال زیر در نظر دارد که متلب وoctave مطمئناً باید توابع متفاوتی برای گرفتن ناحیه از منحنی را استفاده کنند:f(x)=x2cos(x)for-4.در زیر نسخه ای از کد در متلب است:
f = x^2*cos(x);
ezplot (f, [-4, 9](
a =int (f,-4, 9)
disp ( ‘area: ‘), disp (double (a) );
زمانی که فایل را اجرا می کنید، متلب نمودار زیر را ترسیم می کند:
و نتیجه زیر را نشان می دهد:
اما همان ناحیه های یکسان در octave داده شده است، البته شما از بسته نمادین زیر استفاده خواهید کرد:
pkg load symbolic
symbols
x = sym(“x”);
f =inline(“x^2*cos(x)”);
ezplot(f,[—4,9])
print-deps graph.eps
[a, ierror, nfneval]= quad(f,-4,9);
display(‘area: ‘), disp(double(a));
خرید کتاب 28 گام موثر در فتح متلب