گام بیست و سوم: دیفرانسیل متلبی

متلب دستور diff را برای محاسبه مشتقات نمادین فراهم کرده است. ساده ترین شکل، شما می خواهید دیفرانسیل را با دستورdiff به عنوان آرگومان انتقال دهید.

برای مثال، اجازه دهید مشتقی از تابع f(t)=3t²+2t² را محاسبه کنیم.

مثال

یک فایل اسکریپت ایجاد کنید و کد زیر را در آن وارد نمایید:

syms t

f =3*t^2+2*t^(-2);

diff (f)

در زیر معادلات octave محاسبات بالا است:زمانی که کد بالا وارد و اجرا می شود، نتیجه زیر تولید می شود:

pkg load symbolic

symbols

t = sym)”t”(:

f =3*ta2+2*ta (—2(;

differentiate (f, t)

octave کد را اجرا می کند و نتیجه زیر را بر می گرداند:

تایید قوانین ابتدایی دیفرانسیل

اجازه دهید به طور خلاصه وضعیت معادلات مختلف یا قوانین برای دیفرانسیل از تابع و این مقررات را بررسی کنیم. به این منظور، ما f’(x) را برای مشتق مرتبه اول و f”(x) را برای مشتق مرتبه دوم خواهیم نوشت.

در زیر قوانینی برای دیفرانسیل وجود دارد:

قانون 1

برای توابع f و g و اعداد حقیقی a و b مشتقی از تابع هستند:

h(x)=af(x)+bg(x)

با رابطه x داده شده است:

h’(x)=af’(x)+bg’(x)

قانون 2

وضعیت قوانین sum و substraction که اگر f و g دو تابع هستند،f’ و g’ به ترتیب مشتق های آن ها هستند.در آن صورت،

(f+g)’=f’+g’

(f-g)’=f’-g’

قانون 3

قانون product حالت هایی است که اگر f و g دو تابع هستند، f’ و g’ به ترتیب مشتق های آن ها هستند.در آن صورت،

(f.g)’ = f’.g + g’.f

قانون 4

قانون خارج قسمت حالت هایی است که اگر fو g دو تابع باشند، f’ و g’به ترتیب مشتق های آن ها هستند، در آن صورت،

(f/g)’=(f’.g – g’.f)/g²

قانون 5

قوانین چندجمله ای یا نیروی اولیه حالت هایی است که، اگر y=f(x)=xⁿ، در آن صورت f’=n.x^(n-1یک خروجی مستقیم از قوانین مشتق از ثابت صفر است، به عنوان مثال، اگر y=k، هر ثابت، در آن صورت f’=0 است.

قانون 6

قانون chain حالت هایی است که، مشتق تابع از تابع h(x)=f(g(x)) با رابطه x است، h’(x)=f’(g(x)).g’(x)

مثال

یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:

syms x

syms t

f =(x +2)*(x^2+3)

dexl = diff(f)

f =(t^2+3)*(sqxt(t)+ t^3)

dex2 = diff(f)

f =(x^2-2*x +l)*(3*x^3-5*x^2+2)

dex3 = diff(f)

f =(2*x^2+3*x)/(x^3+l)

dex4 = diff(f)

f = (x^2+1) ^17

der5 = diff(f)

f = (t^3+3* t^2+5*t -9) ^ (-6)

der6 = diff(f)

زمانی که فایل را اجرا می کنید، متلب نتیجه زیر را نمایش می دهد:

در زیر معادله octave محاسبه بالا قرار دارد:

pkg load symbolic

symbols

x=sym<“x”>:

t=sym<“t”>:

f =(x +2)*(x^2+3)

der1 = differentiate(f,x)

f =(t^2+3)*(t^(1/2)+ t^3)

der2 = differentiate(f,t)

f =(x^2-2*x +1)*(3*x^3-5*x^2+2)

der3 = differentiate(f,x)

f =(2*x^2+3*x)/(x^3+1)

der4 = differentiate(f,x)

f =(x^2+1)a17

der5 = differentiate(f,x)

f =(t^3+3* t^2+5*t -9)^(-6)

der6 = differentiate(f,t)

مشتقات نمایی، لگاریتمی و توابع مثلثاتی

جدول زیر مشتقات نمایی، لگاریتمی و توابع مثلثاتی را به طور معمولی استفاده می کند:

مشتق	تابع
c^a.x.ln c.a(در لگاریتم طبیعی)	c^a.x
e^x	e^x
1/x	ln x
1/x.ln c	ln_cx
x^x.(1+ln x)	x^x
cos(x)	sin(x)
-sin(x)	cos(x)
sec²(x), or 1/cos²(x) , or 1+tan²(x)	tan(x)
-csc²(x),or -1/sin²(x),or –(1+cot²(x))	cot(x)
sec(x).tan(x)	sec(x)
-csc(x).cot(x)	csc(x)

مثال

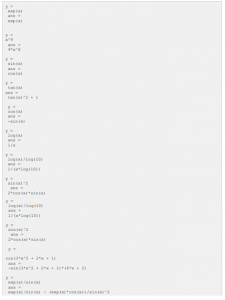
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:

syms x

y = exp(x)

diff(y)

y = x^9

diff(y)

y = sin(x)

diff(y)

y = tan(x)

diff(y)

y = cos(x)

diff(y)

y = loq(x)

diff(y)

y = logl0(x)

diff(y)

y = sin(x)^2

diff(y)

y = cos(3*x^2+2*x +1)

diff(y)

y = exp(x) / sin(x)

diff(y)

زمانی که فایل را ایجاد می کنید، نتیجه زیر نشان داده می شود:

در زیر معادله octave از محاسبات بالا است:

pkg load symbolic

symbols

x = sym(“x”):

y =exp (x)

differentiate(y,x)

y = x^9

differentiate(y,x)

y =sih(x)

differentiate(y,x)

y =tan(x)

differehtiate(y,x)

y =cos(x)

differentiate(y,x)

y =log(x)

differentiate(y,x)

% symbolic packages does hot have this support

%y =logl0(x)

%differentiate(y,x)

y =sih(x)a2

differentiate(y,x)

y =cos(3*xa2+2*x +1)

differentiate(y,x)

y =exp(x)/sih(x)

differentiate(y,x)

محاسبات بالاتر به منظور مشتق

برای محاسبه بالاتری از مشتق تابع f، ما از نحوه اجرا در متلب (diff(f,n استفاده می کنیم.

به ما اجازه دهید مشتق دوم از تابع y=f(x)=x.e^-3x بگیریم.

f = x*exp(-3*x);

diff(f,2)

متلب کد را اجرا خواهد کرد و نتیجه زیر را برمی گرداند:

معادله octave زیر معادل محاسبات بالا است:

pkg load symbolic

symbols

x = sym(“x”):

f = x*exp(-3*x);

differentiate(f, x,2)

مثال

در مثال زیر، ما یک مسئله را حل می کنیم. تابع (y=f(x)=3sin(x)+7cos(5x داده شده است.ما می خواهیم بفهمیم معادله (f”+f=-5cos(2x درست را نگه میدارد.

یک فایل اسکریپت ایجاد کنید و کد زیر را در آن وارد کنید:

syms x

y =3*sin(x)+7*cos(5*x);% defining the function

lhs = diff(y,2)+y;%evaluting the lhs of the equation

rhs =-5*cos(2*x);%rhs of the equation

if(isequal(lhs,rhs))

disp(‘yes, the equation holds true’);

else

disp(‘no, the equation does not hold true’);

end

disp(‘value of lhs is: ‘), disp(lhs);

زمانی که شما فایل را ایجاد می کنید، نتیجه زیر نشان داده می شود:

معادله octave زیر محاسبات بالا را نشان می دهد:

pkg load symbolic

symbols

x = sym(“x”) ;

y =3*sin(x)+7*cos(5*x);% defining the function

lhs = differentiate(y, x,2)+ y;%evaluting the lhs of the equation

rhs =-5*cos(2*x);%rhs of the equation

if(lhs == rhs)

disp(‘yes, the equation holds true’);

else

disp(‘no, the equation does not hold true’);

end

disp(‘value of lhs is: ‘), disp(lhs);

پیدا کردن حداقل و حداکثر از منحنی

اگر ما حداقل و حداکثر را از یک نمودار جستجو کنیم، ما به ط.ر اساسی بیش ترین و کمترین نقاط روی نمودار از یک تابع در محل خاص یا محدوده خاصی از مقادیر از متغیر نمادین را جستجو می کنیم.

برای تابع y=f(x) نقاط روی نمودار که در نمودار شیب صفر دارند نقاط ایستا نامیده می شوند. به عبارت دیگر نقاط ایستا f’(x)=0 هستند.

برای پیدا کردن نقاط ایستا از تابع دیفرانسیل ما ، نیاز به مجموعه مشتق معادله صفر و حل معادلات داریم.

مثال

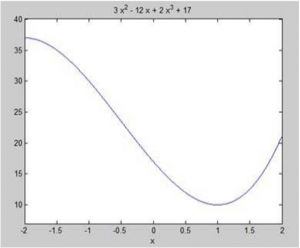
اجازه دهید نقاط ایستا از تابع f(x)=2x³+3x²-12x+17 را در مراحل زیر بگیریم:

1.اول اجازه دهید تابع را وارد کنیم و نمودار آن را رسم کنیم:

syms x

y =2*x^3+3*x^2-l2*x +17;% defining the function

ezplot(y)

متلب کد را اجرا می کند و طرح زیر را برمی گرداند:

اینجا کد معادل octave برای مثال بالا است:

pkg load symbolic

symbols

x = sym )‘ x'( :

y =inline(“2*x^3 + 3*x^2 – l2*x + l7”);

ezplot(y)

print-deps gxaph.eps

فرض ما بر این است که تعدادی محل حداکثر و حداقل روی نمودار وجود دارد، بنابراین ما محل حداکثر و حداقل برای فاصله زمانی[-2,2] را بر روی نمودارنشان می دهیم.

syms x

y =2*x^3+3*x^2-l2*x +17;% defining the function

ezplot (y, [-2, 2])

متلب کد را اجرا خواهد کرد و طرح زیر را بر می گرداند:

اینجا کد معادل octave برای مثال بالا است:

pkg load symbolic

symbols

x = sym )‘ x’);

y =inline(“2*x^3 + 3*x^2 – l2*x + l7”);

ezplot (y, [-2, 2l)

print-deps gxaph.eps

q = diff(y)

بعد ، اجازه دهید مشتق را محاسبه کنیم

متلب کد را اجرا می کند و نتایج زیر را بر می گرداند:

اینجا معادل octave محاسبات بالا است::

pkg load symbolic

symbols

x = ( ii xii) ;

y =2*xa3+3*xa2-l2*x +17;

g = differentiate(y,x)

4. let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

متلب کد را اجرا خواهد کرد و نتیجه زیر را برمی گرداند:

در زیر معادلoctave از محاسبات بالا است:

pkg load symbolic

symbols

x =sym(“x”) ;

y =2*x^3+3*x^2-12*x +17;

g = differentiate(y,x)

roots([6,6,-12])

subs(y,1), subs(y,-2)

این با طرح ما موافق است.بنابراین اجازه دهید تابع f در نقاط بحرانی x=1,-2 را ارزیابی کنیم. ما می توانیم مقدار در تابع نمادین را با استفاده از دستورsubs تعویض کنیم.

متلب کد را اجرا خواهد کرد و نتیجه زیر را بازمی گرداند:

معادل octaveاز محاسبات بالا در زیر آمده است:

pkg load symbolic

symbols

x = sym(“x”) ;

y =2*x^3+3*x^2-12*x +17;

g = differentiate(y,x)

roots([6,6,-12])

subs(y, x,1), subs(y, x,-2)

اغلب مقادیر حداقل و حداکثر بر روی تابع f(x)=2x³+3x²-12x+17، در فاصله زمانی [-2,2] 10و 37 هستند.

حل معادلات دیفرانسیل

متلب دستور dsolve را برای حل معادلات دیفرانسیل نمادین فراهم کرده است.اساسی ترین شکل دستور dsolve برای پیدا کردن راه حل برای یک معادله است:

که eqn یک رشته متنی استفاده شده برای وارد کردن معادله است.این یک راه حل نمادی با یک مجموعه از ثابت های اختیاری که برچسب های متلبc1,c2,و غیره است را باز می گرداند.همچنین شما می توانید شرایط مرزی و اولیه خاصی برای مسئله، به عنوان لیست کاما – جدا از هم معادله چ به صورت زیر :