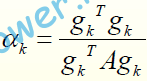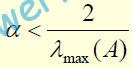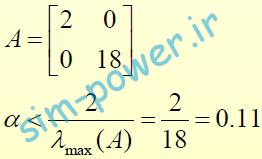روند مينيمم سازي
– الگوريتم كلي
• روند بازگشتي: تخمين جديد از روي تخمين فعلي قابل محاسبه است:
در روشهاي مختلف مينيمم سازي، بردار جستجو متفاوت است.
• (p(k به گونه اي تعيين مي شود كه مقدار تابع F در هر مرحله كاهش يابد.
• بردار جستجو از روي اطلاعات گراديان و هسيان تابع محاسبه مي شود.
– روش بيشترين نزول (SD)
• ديديم كه اگر مسير (p(k در خلاف جهت گراديان باشد، مقدار مشتق جهتي كمترين ميزان ممكن را خواهد داشت.
• در اينجا نيز با توجه به بسط تيلور تابع F حول (x(k به سادگي ديده مي شود كه اگر بردار جستجو در خلاف جهت گراديان انتخاب شود، بيشترين تنزل در مقدار تابع F را خواهيم داشت.
• الگوريتم بيشترين نزول برابر است با:
نكات مربوط به الگوريتم (SD)
• ثابت كنيد نرخ يادگيري بهينه در الگوريتم SD براي توابع درجه دوم عبارتست از:
• مراحل متوالي الگوريتم SD بر هم عمودند.
مثال:
نكات
• با تغيير نرخ يادگيري شكل مسير حركت تغيير مي كند.
• اگر نرخ يادگيري زياد شود سرعت نزديك شدن به نقطه بهينه زيادتر شده ولي ميزان
نوسانات بيشتر خواهد شد.
• اگر ميزان نرخ يادگيري از حدي بيشتر شود، الگوريتم واگرا مي گردد. به اين حد نرخ
يادگيري پايدار گويند.
• براي توابع درجه دوم ثابت مي شود كه نرخ يادگيري پايدار برابر است با
A ماتريس هسيان تابع F
• محاسبه نرخ يادگيري پايدار در مثال قبل
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,