آموزش نرم افزار متلب برای رشته برق – ماتریس (بخش اول)
در این بخش به معرفی روش های مختلف برای تعریف ماتریس پرداخته می شود و دستورات کار کردن با ماتریس ها بیان خواهد شد.
برای ایجاد یک بردار که رابطه بین مقادیر هر عضو آن به صورت تصاعدی است، می توان از روش زیر استفاده نمود:
x= a:b:c <<
a مقدار اولیه،c مقدار نهایی وb مقدار افزاینده است.
x=1:2:10 <<
x = 1 3 5 7 9
x=1:10 <<
x = 1 2 3 4 5 6 7 8 9 10
در صورت لحاظ نکردن عددی برای مقدار افزاینده، همانند نمونه فوق, عدد ۱ در نظر گرفته می شود.
x=(1:2:10) <<
ans = 1 3 5 7 9
علامت ( ) ، عمل فراخوانی را انجام می دهد.
(تعریف بردار) ; x=[1 2 3 4 5 6 7 8 9 10] <<
x=(1:1:5) <<
ans= 1 2 3 4 5
با به کار بردن علامت ; در انتهای دستور، باعث می شود خروجی نشان داده نشود.
y=sin(x) <<
عناصر۳، ۴، ۱، ۲، ۶، ۵ را با همین ترتیب نشان می دهد ;y([3,4,1,2,6,5])<<
عناصر از ۵ به آخر را نشان می دهد. ; x(5:1:end) <<
عناصر را از آخر به اول نشان می دهد. ; x(end:-1:1) <<
Linspace (a, b, c) برای تقسیم بازه (a, b) به تعداد c (تعداد تقسیم + ۱) استفاده می شود.
; f=linspace(0,pi,11) <<
در اینجا متغیر fاز صفر تا π را به ۱۰ قسمت مساوی تقسیم می کند و f دارای ۱۱ عضو است.
اگر تعداد تقسیم ذکر نشود به صورت پیش فرﺽ ۱۰۰ در نظر گرفته می¬شود.
عبارت longspace(a,b,c) برای تقسیم بازه (a,b) بر اساس لگاریتم به تعداد c (تعداد تقسیم + ۱) استفاده می شود.
; logspace(0,2,10)<<
علامت ‘ برای محاسبه ترانهاده یک بردار یا ماتریس استفاده می شود.
; b=[linspace(5,15,7)] <<
;b́ <<
اگر دو ماتریس A و B در محیط نرم افزار تعریف شده باشند، برای ایجاد یک ماتریس جدید حاصل از ادغام این دو ماتریس به صورت زیر عمل می شود:
c=[a b] <<
تعریف ماتریس
برای تعریف ماتریس 3⨯4 زیر چندین روش موجود است:
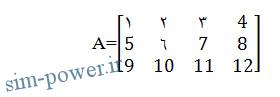
روش اول:
فشردن کلید A= [1 2 3 4 Enter
Enter فشردن کلید 5 6 7 8
9 10 11 12];
روش دوم:
A= [1 2 3 4; 5 6 7 8; 9 10 11 12] <<
روش سوم (بهترین) :
A= [1:4; 5:8; 9:12] <<
برای نمایش آرایه سطر دوم ستون سوم ماتریس فوق به روش زیر استفاده کنید:
; A (2, 3) <<
h=2*A-1 <<
h= [1 3 5 7; 9 11 13 15; 17 19 21 23]
دستورات زیر عنصر سطر پنجم و ستون ششم را برابر ۱۰ قرار می دهد و عناصر مشخص نشده را برابر صفر قرار می دهد.
; A (5, 6) =10 <<
عملگر نقطه (.) باعث می شود عملیات بر روی تک تک آرایه ها به صورت یک به یک انجام پذیرد که این عمل مستلزم هم خوانی سایز ماتریس ها با هم است.

در اینجا برخی از دستوراتی که در کار کردن با ماتریس ها کاربرد دارد، نشان داده شده است:
ضرب نقطه ای ;A. *h <<
عناصر سطر پنجم از ماتریس حذف می شود. [ ]= A (5, 🙂 <<
عناصر ستون ششم از ماتریس حذف می شود. [ ] = A (:, 6) <<
ستون های چهارم تا پنجم از ماتریس حذف می شود. [ ] = A (:, 4:5) <<
عناصر سطر چهارم از ماتریس حذف می شود. [ ] =A (4,:) <<
معکوس ماتریس (در مورد ماتریس های مربعی) ; inv (A) <<
معکوس ماتریس ; A. ^-1<<
معکوس تک تک آرایه ها A. ^-1 <<
دترمینان ماتریس ;det (A) <<
دراین نرم افزار از ( ) ones برای تعریف ماتریس واحد استفاده می شود.
;ones (3)<<
که معادل است با :
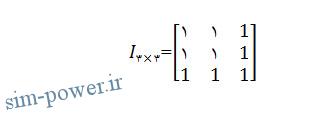
;ones (3, 5)<<
که معادل است با:
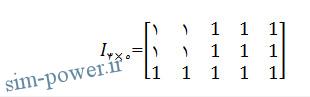
;ones (3, 5, 4)<<
دستور فوق۴ ماتریس واحد ۵⨯۳ در سه بعد تعریف می کند.
; ones (3, 5, 4, 6)<<
در دستور فوق بعد چهارم می تواند زمان باشد.
در این نرم افزار از ( )zeros برای تعریف ماتریس صفر استفاده می شود.
; zeros (3) <<
که معادل است با :
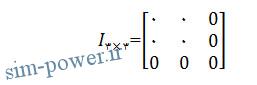
; zeros (3, 4) <<
که معادل است با:
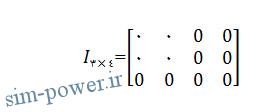
بخش دوم این مطلب را در آموزش نرم افزار متلب برای رشته برق – ماتریس (بخش دوم) مطالعه نمایید.
برای دانلود آموزش این پست به صورت پی دی اف بر روی لینک زیر کلیک کنید.