آموزش متلب, محیط متلب
آموزش نرم افزار متلب برای رشته برق – عملیات بر روی آرایه ها
آموزش نرم افزار متلب برای رشته برق – عملیات بر روی آرایه ها
عملیات ریاضی بر روی ماتریس ها می تواند بر روی تک تک آرایه ها اجرا شود. به این عملیات، عملیات آرایه ای گویند. در این بخش در مورد عملیات آرایه ای صحبت می کنیم . ادامه مطلب را دنبال کنید.
عملیات بر روی آرایه ها
عملیات ریاضی بر روی ماتریس ها می تواند بر روی تک تک آرایه ها اجرا شود. به این عملیات، عملیات آرایه ای گویند. ضرب آرایه ها نمونه ای از آن می باشد. در صورتیکه A و B دو ماتریس با ابعاد یکسان باشند و هریک از اعضاء این دو ماتریس به صورت ai,j و bi,j قابل نمایش باشند، بنابراین فرمان :
C=A.*B <<
ماتریس دیگری به نام C با ابعاد مشابه A و B ایجاد می کند که اعضاء آن به صورت ci,j=ai,j*bi,j هستند. برای مثال استفاده از ماتریس های 3⨯2 با نام های A و B به صورت زیر، مشاهده می شود که :
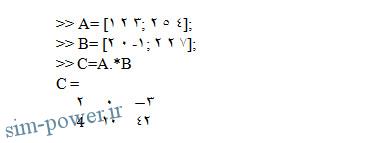
برای به توان رساندن یک عدد اسکالر برای مثال 5 به توان 2، از فرمان 2^5 و در صورتی که هدف انجام عملیات بر روی هر یک از اعضاء یک ماتریس باشد از فرمان 2^. استفاده می شود. برای مثال، در صورتیکه هدف ایجاد ماتریس جدیدی باشد که اعضاء آن مربع اعضاء ماتریس A هستند، می توان نوشت:

تقسیم آرایه ای
همچنین همانگونه که در سایت سیم پاور توضیح دادم یک نوع تقسیم آرایه ای برای دوماتریس هم بعد وجود دارد که دو ماتریس را عضو به عضو برهم تقسیم می کند:
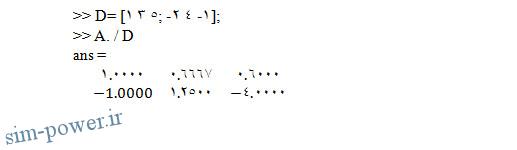
حال توابع sum و cumsum را بررسی می کنیم. این ها توابعی هستند که اغلب با عملگر نقطه (.) به کار می روند. هنگامی که آرگومان تابع sum یک بردار باشد، پاسخ تابع، عددی برابر مجموع تمام آرایه های بردار می باشد و وقتی که آرگومان تابع sum یک ماتریس باشد، پاسخ یک بردار سطری است که هر عضو آن از مجموع اعضای ستون نظیر آن در ماتریس اصلی به دست می آید. پس اگر z یک ماتریس (3⨯4) با اعضای zij باشد، آنگاه :
![]()
یک بردار 4 عضوی است. همین طور
![]()
یک بردار سه عضوی است.
تابع cumsum برای یک بردار v متشکل از n عضو vj که خود بردار n عضوی دیگری است بدین شکل تعریف می شود:
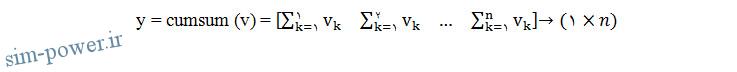
به عبارت دیگر اگر w یک ماتریس (m⨯n) متشکل از اعضای wjk باشد، آنگاه cumsum(w) ماتریس زیر است:
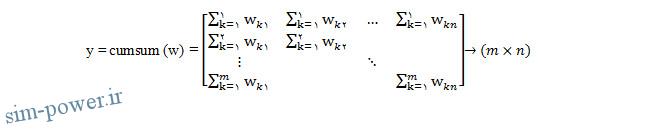
برای نشان دادن کاربرد sum معادله زیر را ملاحظه کنید:
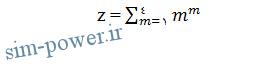
دستور محاسبه عبارت بالا به صورت زیر است:
;m=1:4 <<
;z=sum (m. ^m) <<
هنگامی که دستور فوق اجرا شود، z = 288 را نتیجه می دهد. این دستور را می توان به صورت خلاصه تر نیز نوشت:
; z=sum ((1:4). ^ (1:4)) <<
حال نتایج این قسمت را با محاسبه عبارت زیر برای N=305 و پنج مقدار x از بازهx ≤2 0≤ در فواصل یکسان به طور خلاصه شرح می دهیم:
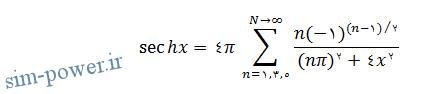
باید همچنین همانگونه که در سایت سیم پاور توضیح دادم مقادیر جمع شده با مقادیر درست مقایسه شود. دستورات زیر را برای محاسبه مثال ذکر شده، اجرا کنید:
nn=1:2:305; %(1⨯153)
xx=linespace(0,2,5); %(1⨯5)
[x,n]=meshgrid(xx,nn); %(153⨯5)
s=4*pi*sum(n.*(-1).^((n-1)/2)./((pi*n).^2+4*x.^2)); %(1⨯5)
se=sech(xx); %(1⨯5)
compare=[s ́ se ́] %(5⨯2)
با اجرا در پنجره فرمان نتیجه می دهد :

تابع meshgrid برای ایجاد ماتریس های (153⨯5) انتخاب شده است که sum جمع تمام سطرها را ستون به ستون انجام می دهد. دستورات بالا را میتوان به صورت خلاصه تر زیر نوشت:
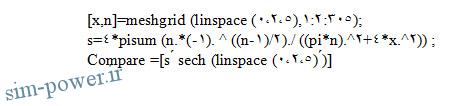
برای دانلود این آموزش به صورت پی دی اف بر روی لینک زیر کلیک کنید.
دانلود فایل عملیات بر روی آرایه ها





