آموزش نرم افزار متلب برای رشته برق – ابزار گرافیکی curve fitting
در این بخش به معرفی ابزار گرافیکی curve fitting و همچنین سری فوریه پرداخته می شود. ادامه مطلب را دنبال کنید.
جعبه ابزار تخمین بهترین منحنی گذرنده از داده ها (CURVE FITTING TOOL)
در این بخش به معرفی ابزار گرافیکی curve fitting پرداخته می-شود. Curve Fitting Tool یک رابط گرافیکی برای اجرای دستورالعمل های زیر است:
ابزاری برای تطابق اطلاعات پراکنده
مشاهده، مقایسه و هموارسازی اطلاعات
درون یابی و برون یابی اطلاعات
با یک مثال به توضیح آن پرداخته می شود. قبل از انجام هر کاری، باید متغیرها در پنجره workspace ایجاد شوند. با اجرای دستورات زیر متغیرهای x و y در فضای کاری ایجاد می شوند.
; x=-pi:0.1:pi<<
; y=x.*sin(x)<<
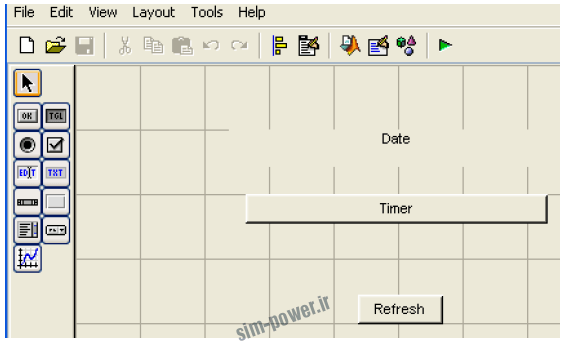
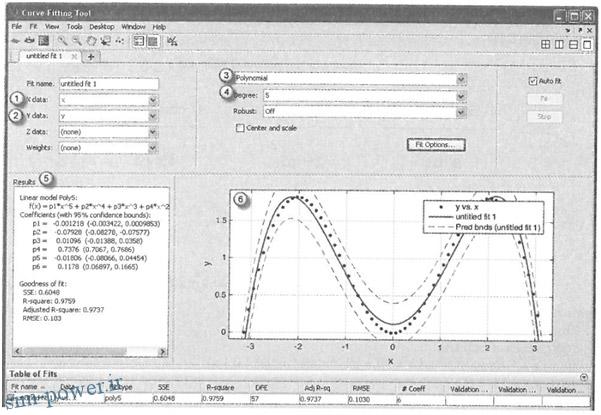
اکنون پنجره Workspace شامل دو متغیر x و y می باشد. حال دستور cftool را در پنجره فرمان وارد کنید یا از قسمت APP نرم افزار بر روی آن کلیک کنید تا به شکل مقابل برسید.

همانطور که ملاحظه می شود، این پنجره از قسمت های مختلفی تشکیل شده است.
ابتدا (مطابق شماره ۱) در قسمت X data عبارت x و (مطابق شماره ۲) در قسمت Y data عبارت y را انتخاب کنید.
سپس (مطابق شماره ۳) نوع معادله و ( مطابق شماره ۴) درجه معادله را انتخاب کنید.
همانطور که مشاهده می شود، امکان انتخاب طیفی وسیع از توابع حتی سری های فوریه معادل نیز وجود دارد.
سپس (مطابق شماره ۵) ضرایب معادله و خطای تقریب منحنی و (مطابق شماره ۶) نمودارهای معادله مورد نظر نشان داده می شود.
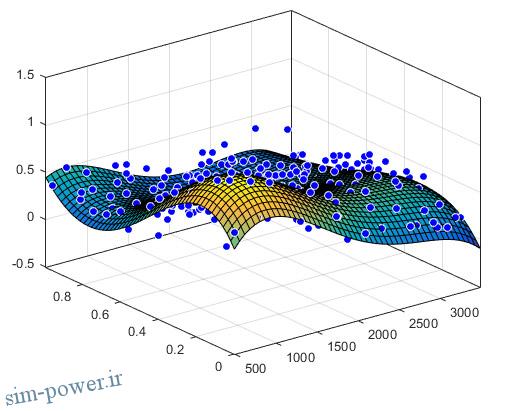
اگر دستورات بالا را اجرا کنید شکلی مطابق روبرو برای شما به نمایش در خواهد آمد.
سری فوریه
سری فوریه با دوره تناوب 2L را به صورت …………………………….. نشان می دهیم.
ضرایب فوریه به ازای …, k=0,1,2 به صورت زیر می باشد.
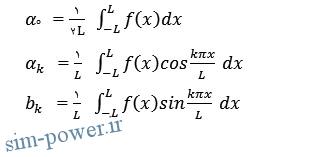
برای محاسبه جمع جزئی تابع f می توان از دستورات زیر در فاصله [-L,L] استفاده کرد، همچنین همانگونه که در سایت سیم پاور توضیح دادم محاسبه ضرایب سینوسی و کسینوسی را می توان در دستورات زیر دنبال نمود:
syms x k L n >>
; evalin(symengine, ́assume(k,Type::Integer) ́)>>
;a = @(f,x,k,L) int(f*cos(k*pi*x/L)/L,x,-L,L) >>
;b = @(f,x,k,L) int(f*sin(k*pi*x/L)/L,x,-L,L) >>
برای محاسبه جمع جزئی تابع f، از دستور زیر استفاده می شود:
… + fs = @(f,x,n,L) a(f,x,0,L)/2<<
;symsum(a(f,x,k,L)*cos(k*pi*x/L) + (b(f,x,k,L)*sin(k*pi*x/L),k,l,n
برای روشن شدن موضوع، دستورات زیر را برای تابع قدرمطلق یا f(x)=abs(x) در پنجره فرمان وارد نمایید. می خواهیم جمع جزئي دهم آن را محاسبه کنیم.
syms x k L n <<
f=abs(x) <<
;a = @(f,x,k,L) int(f*cos(k*pi*x/L)/L,x,-L,L)<<
;b = @(f,x,k,L) int(f*sin(k*pi*x/L)/L,x,-L,L)<<
… +fs=@(f,x,k,L) a(f,x,0,L)/2
;symsum(a(f,x,k,L)*cos(k*pi*x/L) + (b(f,x,k,L)*sin(k*pi*x/L),k,l,n
pretty(fs(f,x,10,1))<<
اگر این کار را انجام دهید، با زدن دکمه Enter به نتایج زیر می رسید
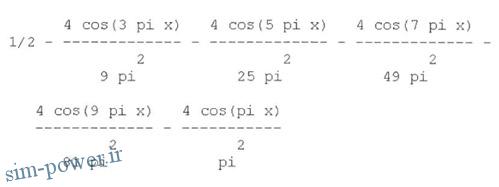
برای رسم جمع جزئی به ازای n=2,5,10 دستورات زیر را در پنجره فرمان اجرا کنید:
syms x k L n <<
f=abs(x) <<
… +fs=@(f,x,k,L) a(f,x,0,L)/2
;symsum(a(f,x,k,L)*cos(k*pi*x/L) + (b(f,x,k,L)*sin(k*pi*x/L),k,l,n
ezplot(fs(f,x,2,1),-1,1) <<
hold on
ezplot(f,-1,1) <<
hold off
title( ́Partial sum with n=2 ́)<<
برای رسم جمع جزئی به ازای n=5 دستورات زیر را در پنجره فرمان اجرا کنید:
syms x k L n <<
f=abs(x) <<
…+fs=@(f,x,k,L) a(f,x,0,L)/2
;symsum(a(f,x,k,L)*cos(k*pi*x/L) + (b(f,x,k,L)*sin(k*pi*x/L),k,l,n
ezplot(fs(f,x,5,1),-1,1)<<
hold on
ezplot(f,-1,1) <<
hold off
title( ́Partial sum with n=5 ́) <<
برای رسم جمع جزئی به ازای n=10 دستورات زیر را در پنجره فرمان اجرا کنید:
syms x k L n <<
f=abs(x)<<
… + fs=@(f,x,k,L) a(f,x,0,L)/2
;symsum(a(f,x,k,L)*cos(k*pi*x/L) + (b(f,x,k,L)*sin(k*pi*x/L),k,l,n
ezplot(fs(f,x,10,1),-1,1) <<
hold on
ezplot(f,-1,1)<<
hold off
title( ́Partial sum with n=10 ́)<<
برای دانلود این آموزش به صورت پی دی اف بر روی لینک زیر کلیک کنید.