آکادمی سیم پاور
گام بیست و یکم: جبر در متلب
گام بیست و یکم: جبر در متلب
تا حالا، ما تمامی مثال های کاری در متلب و همچنین gnu را مشاهده کردیم، متناوباً octave نامیده می شوند.
اما برای حل معادلات جبری پایه ، متلب و octave اختلاف کمی دارند، بنابراین ما سعی می کنیم متلب و octave را در بخش جداگانه ای پوشش دهیم.
دستور solve برای حل معادلات جبری استفاده شده است. در ساده ترین، حل معادله در نقل قول محصور است.
برای مثال، اجازه دهید x را در معادله x-5=0 حل کنیم
![]()
متلب عبارات بالا را اجرا خواهد کرد و نتیجه زیر را برمی گرداند:
![]()
همچنین شما می توانید با فراخوانی تابع به این صورت آن را حل کنید:
![]()
مطلب دستورات بالا را اجرا می کند و نتیجه زیر را برمی گرداند:
![]()
شما ممکن است حتی طرف راست معادله را نداشته باشید:
مطلب دستورات بالا را اجرا می کند و نتیجه زیر را برمی گرداند:
اگر معادله شامل چند نماد است، در آن صورت متلب به طور پیش فرض فرض می کند شما برای x حل می کنید، اگرچه، دستورsolve شکل دیگری دارد:
که در آن، شما می توانید متغیرها را ذکر کنید.
برای مثال، اجازه دهید معادله v-u-3t2=0، برای v حل کنیم.
مطلب دستورات بالا را اجرا می کند و نتیجه زیر را برمی گرداند:
حل معادله جبری پایه در ctave
دستور root برای حل معادله جبری در octave استفاده می شود و شما می توانید مثال های بالا را به صورت زیر بنویسید:
برای مثال، اجازه دهید x را در معادله x-5=0 حل کنیم:
roots([l,-5])
همچنین می توانید تابع حل را به این صورت فراخوانی کنید:octave دستورات بالا را اجرا خواهد کرد و نتیجه زیر را برمی گرداند:
y = roots([l,-5])
octave دستورات بالا را اجرا خواهد کرد و نتیجه زیر را بر می گرداند:
حل معادلات در جه دوم در octave
مثال زیر معادله درجه دوم x2-7x+12=0 را در octave حل می کند.یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
s = roots([l,-7,12]);
disp(‘the first root is: ‘), disp(s(l));
disp(‘the second root is: ‘), disp(s(2));
زمانی که شما فایل را اجرا می کنید، نتیجه زیر نشان داده می شود:
حل معادلات درجه دوم به کمک متلب
دستور solve همچنین می تواند معادله مرتبه بالاتر را حل کند. اغلب برای حل معادلات درجه دوم استفاده می شود. تابع ریشه هایی از معادلات در آرایه را برمی گرداند.
مثال زیر معادله درجه دوم x2-7x+12=0 را حل می کند.یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
eq =‘x^2 -7*x + 12 = 0′;
s = solve(eq);
disp(‘the first root is: ‘), disp(s(l));
disp(‘the second root is: ‘), disp(s(2));
زمانی که شما فایل را اجرا می کنید، نتیجه زیر نشان داده می شود:
دستور solve همچنین می تواند معادلات مرتبه بالاتر را حل کند. برای مثال، اجازه دهید یک معادله مکعبی به صورت
x-3)2(x-7)=0) را حل کنیم:
solve(‘(x-3)^2*(x-7)= 0‘)
متلب دستورات بالا را اجرا می کند و نتایج زیر را بر می گرداند:
در رابطه با معادلات مرتبه بالاتر ، ریشه ها حاوی شرایط بیشتر و بلندی هستند. شما می توانید مقادیر عددی مانند ریشه ها را با تبدیل آن ها double کنید.مثال زیر معادله مرتبه چهارx4-7x3+3x2-5x+9=0 را حل می کند.
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
eq =‘x^4 – 7*x^3 + 3*x^2 – 5*x + 9 = o’;
s = solve(eq);
disp(‘the first root is: ‘), disp(s(l));
disp(‘the second root is: ‘), disp(s(2));
disp(‘the third root is: ‘), disp(s(3));
disp(‘the fourth root is: ‘), disp(s(4));
% converting the roots to double type
disp(‘numeric value of first root’), disp(double(s(l)));
disp(‘numeric value of second root’), disp(double(s(2)));
disp(‘numeric value of third root’), disp(double(s(3)));
disp(‘numeric value of fourth root’), disp(double(s(4)));
زمانی که فایل را ایجاد می کنید، نتیجه زیر برگردانده می شود:
لطفاً به دو ریشه آخر توجه داشته باشید که ارقام پیچیده ای هستند.
حل معادلات مرتبه بالاتر در octave
مثال زیر معادله مرتبه چهار x4-7x3+3x2-5x+9=0 را حل می کند.
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
v :[l,·7, 3,-5, 9]:
s = roots(v);
% converting the roots to double type
disp(‘numeric value of first root’), disp(double(s(l)));
disp(‘numeric value of second root’), disp(double(s(2)));
disp(‘numeric value of third root’), disp(double(s(3)));
disp(‘numeric value of fourth root’), disp(double(s(4)));
زمانی که شما فایل را اجرا می کنید، نتیجه زیر را بر می گرداند:
سیستم حل معادلات در متلب
دستور solve همچنین می تواند برای تولید راه حل هایی از سیستم معادله شامل بیش از یک متغیر استفاده شود. اجزه دهید از یک مثال ساده برای اثبات آن استفاده کنیم.
اجازه دهید این معادله را حل کنیم:
5x+9y=5
3x-6y=4
یک فایل اسکریپت ایجاد کنید و کد زیر را تایپ نمایید:
s = solve(‘5*x + 9*y = 5‘,‘3*x – 6*y = 4‘);
s . x
s . y
زمانی که شما فایل را ایجاد می کنید، نتیجه زیر نمایش داده می شود.
با همین روش شما می توانید سیستم های خطی بزرگتری را حل نمایید.مجموعه معادلات زیر را در نظر داشته باشید:
x+3y-2z=5
3x+5y+6z=7
2x+4y+3z=8
سیستم حل معادلات در octave
ما روش های اندک متفاوتی برای حل سیستم از معادلات خطی’n’در ‘n’ مجهول داریم.اجازه دهید از یک مثال ساده برای نمایش آن استفاده کنیم.
اجازه دهید معادلات زیر را حل کنیم:
5x+9y=5
3x-6y=4
همچنین یک سیستم از معادلات خطی می تواند به عنوان معادله ماتریس مجرد ax=b نوشته شود، که a ضریب ماتریس است، b بردار ستونی که حاوی سمت راست معادله خطی است و x بردار ستونی نشان دهنده راه حل که در برنامه زیر نشان داده می شود:
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید:
a =[5, 9;3,-6];
b = [5 ; 4] ;
a \ b
زمانی که شما فایل را اجرا می کنید، نتیجه زیر نشان داده می شود:
با همین روش، شما می توانید سیستم های خطی بزرگتر به صورت داده شده در زیر را حل نمایید:
x+3y-2z=5
3x+5y+6z=7
2x+4y+3z=8
گسترش و جمع آوری معادلات در متلب
دستور expand و collect به ترتیب گسترش و مجموع معادله است. مثال زیر این مفهوم را شرح می دهد:
زمانی که شما با بسیاری از توابع نمادین کار می کنید، شما باید متغیرهای نمادین را تعریف نمایید.
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
syms x %symbolic variable x
syms y %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3*(x-7))
collect(x^4*(x-3)*(x-5))
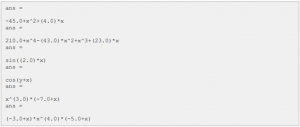
زمانی که شما فایل را اجرا می کنید، نتایج زیر نشان داده می شوند:
گسترش و جمع آوری معادلات در octave
شما به بسته symbolicنیاز دارید، که دستور collect و expand را به ترتیب برای گسترش و جمع آوری فراهم کند. مثال زیر این مفهوم را تشریح می کند:
زمانی که شما با تعدادی از توابع نمادین کار می کنید، شما باید متغیرهای نمادین را تعریف کنید اما octave روش های متفاوتی برای تعریف متغیرهای نمادین دارد.توجه کنید که از sin و cos استفاده شده است، آن ها نیز در بسته نمادین تعریف شده اند.
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
% first of all load the package, make sure its installed.
pkg load symbolic
% make symbols module available
symbols
% define symbolic variables
x = sym (‘x‘);
y = sym )‘y‘(;
z = sym (‘z‘);
% expanding equations
expand((x-5)*(x+9((
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
% collecting equations
collect(x^3*(x-7), z)
collect(x^4*(x-3)*(x-5), z)
زمانی که شما فایل را ایجاد می کنید، نتیجه زیر نمایش داده می شود:
تجزیه و ساده سازی عبارات جبری
دستور factor فاکتور بیان و دستور simply ساده سازی را بیان می کند. مثال زیر این مفهوم را تشریح می کند:
مثال
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ کنید:
syms x
syms y
factox(xa3- ya3)
factox([xa2-ya2,xa3+ya3])
simplify((xa4-16)/(xa2-4))
زمانی که فایل را ایجاد می کنید، نتیجه زیر نشان داده می شود:
خرید کتاب 28 گام موثر در فتح متلب