نمودار های خاص در متلب - سیم پاور (گروه مهندس عربعامری)

رسم نمودار دایره ای (نمودار کلوچه ای – pie plot) با دستور pie در متلب :

حتما تاکنون نمودار دایره ای را مشاهده نموده اید که در آن یک دایره بزرگ به بخش های مختلف، با رنگ های متفاوت، تقسیم می شود و نام هر قسمت و درصد مربوط به آن نیز در کنار آن قسمت نمایش داده می شود. برای نمایش یک نمودار دایره ای (pie plot)، از دستور pie در متلب، استفاده می شود. به مثال زیر توجه کنید :

مثال :

فرض کنید بخواهیم آمار مردان و زنان یک روستا را، با استفاده از یک نمودار دایره ای (pie plot)، نمایش بدهیم. فرض می کنیم 60 درصد مردم روستا، مرد و 40 درصد مردم روستا، زن باشند. کدهای زیر را می نویسیم :

data=[60,40]
pie(data)

نتیجه :

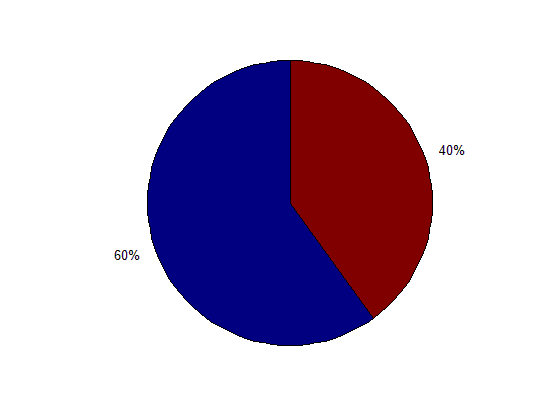
اختصاص دادن نام به هر قسمت از نمودار دایره ای (pie plot) :

ممکن است که بخواهیم، نام هایی دلخواه را به بخش های مختلف نمودار دایره ای (pie plot) اختصاص بدهیم، برای این منظور باید نام ها را درون پرانتز دستور pie ذکر کنیم. به مثال زیر توجه کنید :

مثال :

همان مثال قبل را، این بار با انتخاب دو نام برای دو قسمت نمودار میله ای، تکرار می کنیم :

data=[60,40]
pie(data,{‘man 60%’,’woman 40%’})

نتیجه :

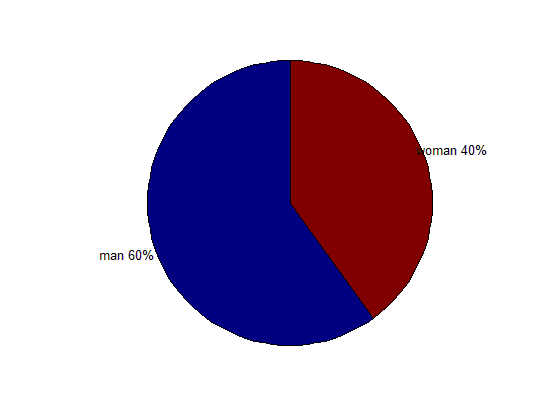
مشاهده می کنید که در کنار هر قسمت، نام انتخاب شده برای آن، نمایش داده شده است.

تعیین نوع رنگ های نمایش داده شده برای نمودار دایره ای با دستور colormap :

در متلب، مجموعه های مختلفی از رنگ ها برای نمایش وجود دارد. هر کدام از این مجموعه رنگ ها را می توان با استفاده از دستور colormap در متلب، انتخاب نمود تا شکل، با آن مجموعه رنگ ها، ترسیم شود. مجموعه رنگ های موجود در متلب و نام معادل برای آنها، در شکل زیر نمایش داده شده است :

در نرم افزار متلب، مجموعه رنگ پیش فرض برای نمایش شکل ها، مجموعه رنگ های jet می باشد. یعنی اگر از دستور colormap استفاده نشود، به طور پیش فرض، شکل با مجموعه رنگ های jet رسم می شود.

به مثال زیر توجه کنید :

مثال :

همان مثال قبل را، این بار با مجموعه رنگ cool ، رسم می کنیم :

data=[60,40]
pie(data,{‘man 60%’,’woman 40%’})
colormap cool

نتیجه :

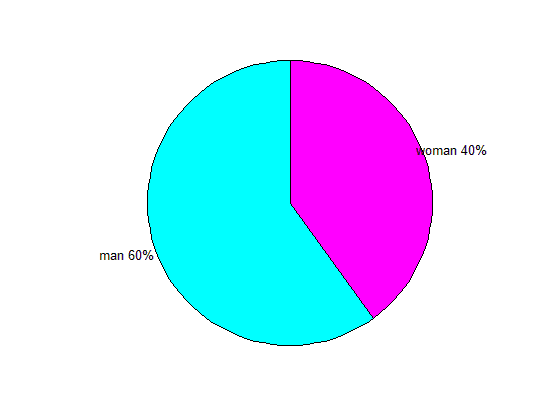
مشاهده می کنید که رنگ های دیگری (مجموعه cool) برای نمایش نمودار دایره ای (pie plot) به کار رفته است.

دقت کنید که نام های قسمت های مختلف نمودار دایره ای درون علامت های { و } قرار داده شده اند.

برجسته کردن قسمتی از نمودار دایره ای (pie plot) :

گاهی برای توجه بیشتر به یک قسمت از نمودار دایره ای (pie plot)، آن قسمت را از نمودار کمی بیرون می آورند تا به صورت برجسته تر نمایش داده شود. برای این منظور، باید برداری با نام explode بسازیم و به بخش متناظر با قسمتی که می خواهیم برجسته شود، عدد 1 و به سایر بخش ها، عدد 0 را اختصاص بدهیم. برای روشن شدن مطلب، به مثال زیر توجه کنید :

مثال :

همان مثال قبل را، این بار با برجسته کردن بخش مربوط به آمار زنان، تکرار می کنیم :

data=[60,40]
explode=[0,1]
pie(data,explode,{‘man 60%’,’woman 40%’})
colormap cool

نتیجه :

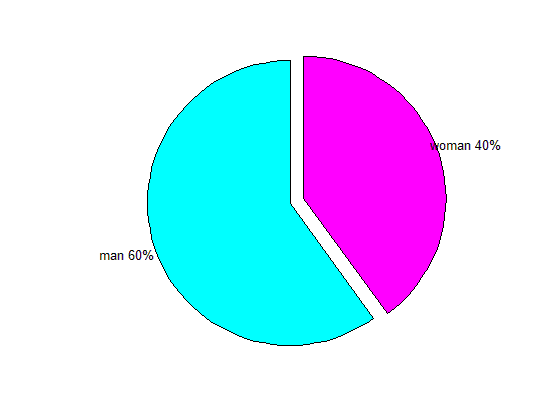
مشاهده می کنید که بخش آمار مربوط به زنان، از دایره کل، جدا بوده و کمی به سمت بیرون دایره پیش رفته است.

رسم هیستوگرام زاویه ای (Angle histogram) با دستور rose در متلب :

قبل از توضیح در مورد هیستوگرام زاویه ای (Angle Histogram)، بهتر است هیستوگرام مستطیلی (Rectangle Histogram) را توضیح بدهیم تا بعد از آن، درک هیستوگرام زاویه ای، آسان تر باشد. شکل زیر، یک هیستوگرام مستطیلی (Rectangle Histogram) می باشد :

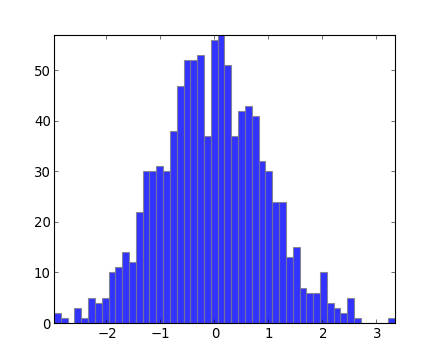
هیستوگرام فوق، از یک جامعه آماری به دست آمده است. در هیستوگرام مستطیلی (Rectangle Histogram)، میله هایی با ارتفاع های مختلف، در کنار هم نشان داده می شوند. در زیر هر میله، نوشته شده است که آن میله، برای کدام بخش از جامعه آماری (با یک ویژگی خاص) می باشد و یا اینکه مقادیر آن را از نزدیک ترین عدد می توان تشخیص داد. محور افقی، نشان دهنده ویژگی درنظر گرفته شده برای آن جامعه می باشد و ارتفاع هر میله نیز نشان دهنده تعداد اعضایی از جامعه آماری می باشد که آن ویژگی را داشته اند.

حال هیستوگرام زاویه ای (Angle Histogram) را توضیح می دهیم. با یک مثال نشان می دهیم که برای چه مسائلی بهتر است به جای هیستوگرام مستطیلی (Rectangle Histogram) ، از هیستوگرام زاویه ای (Angle Histogram) برای نمایش اطلاعات آماری استفاده کنیم :

مثال :

فرض کنید بخواهیم آماری از لکه های خورشیدی دیده شده بر روی خورشید را بر حسب مکان آنها نمایش بدهیم. شکل خورشید را با یک خط افقی بر روی آن در نظر بگیرید :

فرض کنید شکل خورشید را که یک دایره می باشد، به 8 قسمت به صورت زیر تقسیم کنیم :

هر لکه خورشیدی را که مشاهده کنیم، تنها کافی است که زاویه آن لکه خورشیدی، نسبت به خط افقی را یادداشت کنیم. بعدا با دیدن آن زاویه، به راحتی تشخیص می دهیم که آن لکه خورشیدی، در کدام قسمت از 8 قسمت تشخیص داده شده، قرار داشته است.

حال می خواهیم که با یک هیستوگرام زاویه ای (Angle Histogram)، نشان بدهیم که توزیع لکه های خورشیدی، در این 8 بخش، به چه صورت بوده است. کد های زیر را می نویسیم :

theta=[pi*(1/16) pi*(1/16) pi*(1/16) pi*(3/8) pi*(7/8) pi*(7/8) pi*(11/8) pi*(13/8) pi*(13/8)];
rose(theta,8)

نتیجه :

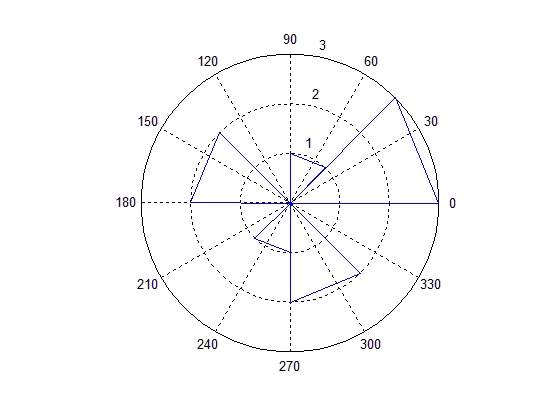
عدد 8 ، درون پرانتز دستور rose ، تعیین کرده است که دایره باید به 8 قسمت مساوی تقسیم شود. همچنین زاویه های لکه های خورشیدی را در بردار theta نوشته ایم. نماد pi برای عدد مشهور پی ( Π ) به کار می رود و زاویه ها را به صورت ضرایبی از عدد پی ( Π ) نوشته ایم. تعداد زوایا برای هر قسمت را در جدول زیر نمایش داده ایم :

قسمت	تعداد لکه های خورشیدی
قسمت اول	3
قسمت دوم	1
قسمت سوم	0
قسمت چهارم	2
قسمت پنجم	0
قسمت ششم	1
قسمت هفتم	2
قسمت هشتم	0

همان طور که مشاهده می کنید، در هیستوگرام زاویه ای (Angle Histogram)، برای هر قسمت (قسمت 45 درجه ای) که آمار آن غیر صفر باشد، یک مثلث، نمایش داده شده است و برای قسمت هایی که در آنها، لکه خورشیدی مشاهده نشده است و زاویه ای مربوط به آنها در بردار theta ذکر نشده باشد، هیچ مثلثی نمایش داده نمی شود تا بدانیم که آمار این قسمت ها برابر صفر بوده است.

در هیستوگرام زاویه ای (Angle Histogram)، هر چه ضلع سوم مثلث، به بزرگترین دایره نزدیک تر باشد، یعنی آمار شمارش برای آن قسمت، بیشتر بوده است. همچنین، عدد مربوط به تعداد هر قسمت، در کنار دایره هایی که با خط چین نمایش داده شده اند، نوشته شده است.

رسم نمودار نایکوئیست با دستور nyquist در متلب :

نمودار نایکوئیست، در درس های کنترل خطی و پردازش سیگنال، به کار می رود و معمولا برای بررسی پایداری سیتم های دارای فیدبک استفاده می شود. نمودار نایکوئیست یک تابع، به این صورت رسم می شود که قسمت حقیقی تابع، بر روی محور افقی و قسمت موهومی تابع، بر روی محور عمودی رسم می شود، اما این می شود یک نقطه به ازای یک فرکانس خاص و چون تابع، تابعی از فرکانس است، این تابع را برای فرکانس های مختلف رسم می کنیم که نتیجه آن، به صورت خط های نمودار نایکوئیست می باشد. دستور nyquist در متلب، برای رسم نمودار نایکوئیست یک تابع، به کار می رود. به مثال زیر توجه کنید :

مثال :

فرض کنید بخواهیم نمودار نایکوئیست تابع زیر را رسم کنیم :

H (s) = 2 s 2 + 5 s + 1 s 2 + 2 s + 3

کدهای زیر را می نویسیم :

clear all
close all
clc

H=tf([2 5 1],[1 2 3])
nyquist(H)

ضرایب صورت و مخرج تابع را به دستور tf می دهیم، تا تابع را بسازد و سپس نمودار نایکوئیست تابع ساخته شده را با دستور nyquist رسم می کنیم.

نتیجه :

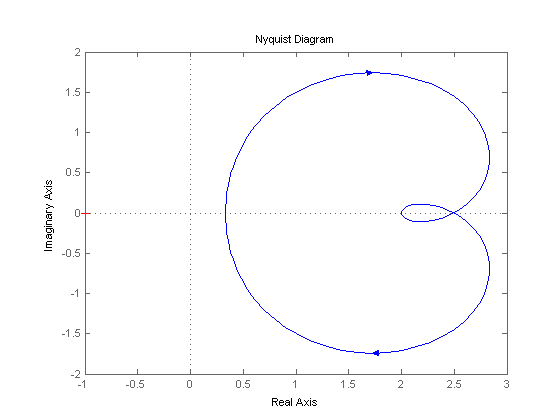
مشاهده می کنید که خود دستور nyquist ، عنوان های محورها را مشخص کرده است.

نکته :

شاید بخواهید مقادیر قسمت های حقیقی و موهومی تابع را برای یک فرکانس خاص بیابید، برای این منظور ،تنها کافی است که در بالای پنجره شکل باز شده، بر روی گزینه Data Cursor به شکل کلیک کنید و سپس بر روی یک نقطه از نمودار، کلیک کنید، تا اطلاعات مربوط به آن نقطه، یعنی فرکانس و بخش های حقیقی و موهومی تابع در آن نقطه، نمایش داده شود. نتیجه به صورت شکل زیر می باشد :

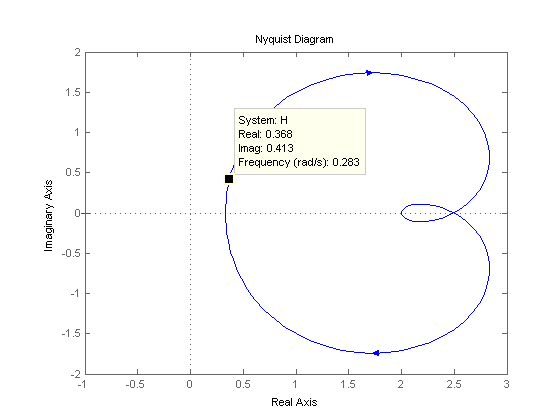
نکته :

با استفاده از دستور grid ، می توانیم دوایر M (M circles) را در نمودار نایکوئیست رسم کنیم. به مثال زیر توجه کنید :

مثال :

همان مثال قبل را این بار با دستور grid می نویسیم :

clear all
close all
clc

H=tf([2 5 1],[1 2 3])
nyquist(H)
grid

نتیجه :

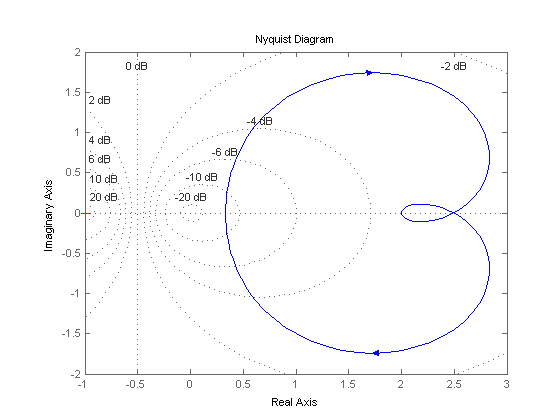
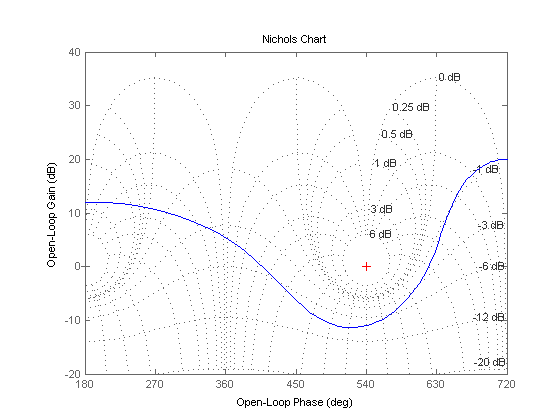
رسم نمودار نیکولز (nichols) با دستور nichols در متلب :

نمودار نیکولز (nichols)، در درس های کنترل خطی و پردازش سیگنال به کار می رود و معمولا برای بررسی پایداری سیتم های دارای فیدبک استفاده می شود. در نمودار نیکولز (nichols) ، عبارت

20 l o g 10 (| H (s) |)

بر حسب

a r g (H (s))

رسم می شود. دقت شود که برای هر فرکانس، یک نقطه خواهیم داشت و با رسم کردن نقاط مربوط به فرکانس های مختلف، خطوطی به صورت نمودار نیکولز (nichols)، نمایش داده می شوند. دستور nichols در متلب، برای رسم نمودار نیکولز (nichols) به کار می رود. به مثال زیر توجه کنید :

مثال :

clear all
close all
clc

H=tf([-4 48 -18 250 600],[1 30 282 525 60])
nichols(H)

ضرایب صورت و مخرج تابع را به دستور tf می دهیم، تا تابع را بسازد و سپس نمودار نیکولز تابع ساخته شده را با دستور nichols رسم می کنیم.

نتیجه :

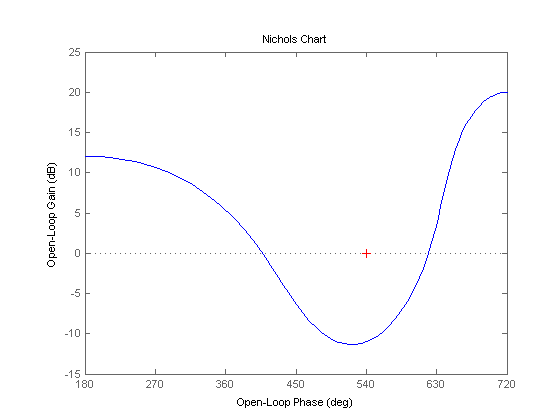
نکته :

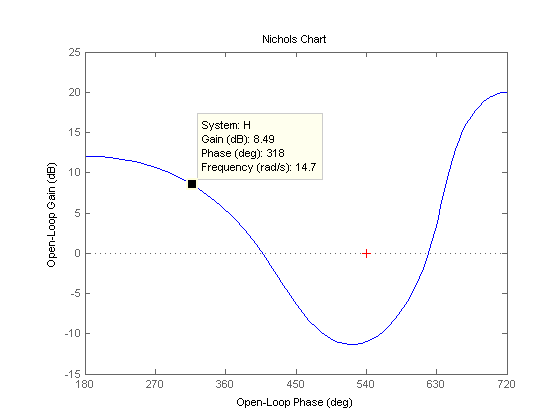
چنانچه بخواهید مقادیر مورد نظر را برای یک فرکانس خاص بیابید، برای این منظور، تنها کافی است که در بالای پنجره شکل باز شده، بر روی گزینه Data Cursor به شکل کلیک کنید و سپس بر روی یک نقطه از نمودار، کلیک کنید، تا اطلاعات مربوط به آن نقطه، از جمله فرکانس، نمایش داده شود. نتیجه به صورت شکل زیر می باشد :