رسم نمودار سه بعدی در متلب
تابع plot3 براي رسم نمودار در فضا به كار مي رود. توجه داشته باشيد كه نتيجه ي استفاده از اين دستور نيز يك خط است ، با اين تفاوت كه اين خط داراي بعد بوده و در يك محور سه بعدي رسم مي گردد . تفاوت كار با اين نمودار آنست كه سه متغير به آن داده مي شود كه متغير اول محورx، متغير دوم محورy و متغير سوم محور z را تعيين مي كند. توجـه داشـته باشيد كه هر سه متغير بايد م اتريسهاي سطري با طول برابر باشند. در اينجا حتماً بايد حداقل سه متغير مربوط بـه سـه محـور وارد شوند . پس از سه ورودي اصلي، مي توانيد عبارات مربوط به ويرايش نمودار را نيز وارد كنيد . نمودار حاصله سه بعـدي بوده و پس از رسم، با فعال كردن ابزار از نوار ابزار بالاي پ نجره ي figures و تغيير شكل موس به صورت يـك دايـره، ميتوانيد كليد سمت چپ موس را در حالي كه موس را روي نمودار قرار داده اي د نگه داريد، و با حركت دادن آن بـه اطـراف، نمودارتان را بچرخانيد و از جهت هاي ديگر نيز آنرا بررسي كنيد . اگر در اين شرايط روي نمودار كليك راس ت كنيد، امكاناتي عبارت از برگرداندن شكل به نماي اوليه (Reset To Orginal View)، ديدن شكل از نماي يكي از صفحه ها(Y-Z ، X-Y يا X-Z و ) امكاناتي براي تنظيم چگونگي چرخش محور و نمودار (Rotate Option) ، در اختيار شما قرار مي گيرد . براي آنكه از هم اندازه بودن ط ول متغيرهاي م اتريسيمان اطمينان حاصل كنيم مي توانيم از روشهاي گوناگوني استفاده كنيم . قرار دادن يك متغير واسط(مثلاً t) ، تعريف يك متغير و تابع قرار دادن بقيه ي متغيرها به آن و يا استفاده از توابـع length و linspace از آن جمله اند. به نمونه هايي از نمودارهايي كه با استفاده از دستور plot3 رسم شده اند توجه كنيد:
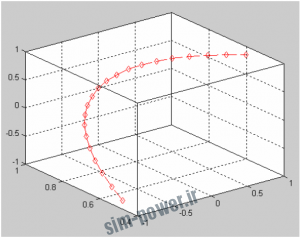
>> t=-1:.1:1;
>> x=sin(t);
>> y=cos(t);
>> z=t;
>> plot3(x,y,z,’–rd’)
>> grid on
>> box on
نوشتن دستور grid on پس از دستور plot3 موجب اِسكِيل بندي صفحه شده اسـت . دسـتور box on باعث مي گردد كه محور نمودار به صورت يك جعبه ي شفاف در آيد كه اين حالت نمودار، تجسم شكل سه بعدي را راحتتـر مي كند . توجه داشته باشيد كه دستورات ويرايش نمودار و يا محور آن، پس از دستور plot3 بايد نوشته شـو ند تـا روي آن أت ثيرگذار باشند.
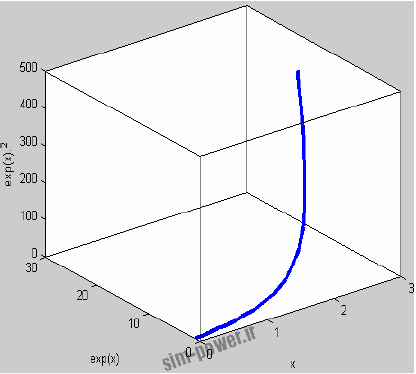
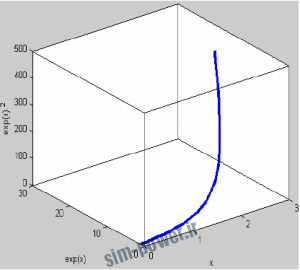
>> x=0:.1:3;
>> y=exp(x);
>> z=y.^2;
>> plot3(x,y,z,’linewidth’,3)
>> xlabel(‘x’); ylabel(‘exp(x)’); zlabel(‘exp(x).^2’);
>> box on
دستورات ylabel ،xlabel وzlabel براي آنست كه روي محورهايمان نام بگذاريم تا روي تصوير بتوانيم آنهـا را بهتـر پيدا كنيم .
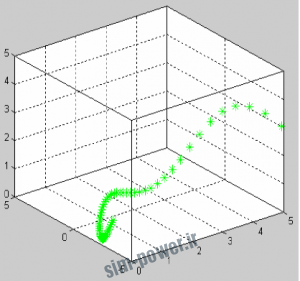
>> a=-pi:pi/18:pi;
>> b=logspace(-1,1,length(a));
>> c=sin(a)+cos(b);
>> plot3(b,a,c,’g*’)
>>grid on
>>box on
>>xlim([0,5]);ylim([-5,5]);zlim([0,5]);
توابع محدود كننده ي محورها را در مثال فوق مشاهده نموديد . اين توابع كه ورودي آنها حدود هر محور را تعيين مي كند، براي يك نمودار سه بعدي ylim ،xlim و zlim هستند.
نویسنده: پور مقدس
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,