رسم مقادیر یک ماتریس دو بعدی به صورت نواری (ribbon)، با دستور ribbon در متلب :
با دستور ribbon در متلب، می توانیم مقادیر عناصر یک ماتریس دو بعدی را به صورت نواری (ribbon) رسم کنیم. به مثال زیر توجه کنید :
مثال :
close all
clc
x=-4:0.5:4;
y=-4:0.5:4;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
ribbon(y,z)
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

نکته :
چنانچه بخواهیم مقادیر عددی متناظر با رنگ نوار ها را بدانیم، می توانیم با دستور colorbar ، این مقادیر را در کنار شکل نمایش بدهیم. به مثال زیر توجه کنید :
مثال :
همان مثال قبل را این بار با دستور colorbar می نویسیم :
close all
clc
x=-4:0.5:4;
y=-4:0.5:4;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
ribbon(y,z)
colorbar
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

مثال :
مثال خود نرم افزار متلب :
close all
clc
[x,y] = meshgrid(-3:.5:3,-3:.1:3);
z = peaks(x,y);
ribbon(y,z)
xlabel(‘X’)
ylabel(‘Y’)
zlabel(‘Z’)
colormap hsv
نتیجه :
رسم مقادیر یک ماتریس دو بعدی به صورت آبشاری (waterfall)، با دستور waterfall در متلب :
با دستور waterfall در متلب، می توانیم مقادیر عناصر یک ماتریس دو بعدی را به صورت آبشاری (waterfall) رسم کنیم. به مثال زیر توجه کنید :
مثال :
close all
clc
x=-8:0.5:8;
y=-8:0.5:8;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
waterfall(x,y,z)
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

نکته :
چنانچه بخواهیم مقادیر عددی متناظر با رنگ سیم ها را بدانیم، می توانیم با دستور colorbar ، این مقادیر را در کنار شکل نمایش بدهیم. به مثال زیر توجه کنید :
مثال :
همان مثال قبل را این بار با دستور colorbar می نویسیم :
close all
clc
x=-8:0.5:8;
y=-8:0.5:8;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
waterfall(x,y,z)
colorbar
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

مثال :
مثال خود نرم افزار متلب :
close all
clc
[X,Y,Z] = peaks(30);
waterfall(X,Y,Z)
نتیجه :

حذف (عدم نمایش) خط های مربوط به رسم سیمی (دستوراتی مثل mesh و meshc و …) مقادیر یک ماتریس دو بعدی، هنگام قرار گرفتن در پشت سایر خط ها، با دستور hidden در متلب :
همان طور که می دانید، دستوراتی مثل mesh و meshc و … در متلب، برای رسم مقادیر یک ماتریس دو بعدی به صورت سیمی (mesh) به کار می رود. با استفاده از دستور hidden ، می توانیم خط هایی (سیم هایی) که پشت سر سایر خط ها قرار می گیرند را حذف کنیم. یعنی با اجرای دستور زیر :
اما بدون اجرای دستور فوق نیز، به طور پیش فرض، این خط ها حذف می شوند (یعنی به صورت پیش فرض، hidden به صورت on در نظر گرفته می شود)، اما چنانچه دستور زیر را اجرا کنیم، خط هایی که پشت سر سایر خط ها قرار می گیرند نیز نمایش داده می شوند :
برای درک بهتر این موضوع، به مثال زیر توجه کنید :
مثال :
ابتدا با hidden on ، یک شکل را رسم می کنیم :
close all
clc
x=-8:0.5:8;
y=-8:0.5:8;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
mesh(x,y,z)
hidden on
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

اکنون همان مثال را با hidden off می نویسیم :
close all
clc
x=-8:0.5:8;
y=-8:0.5:8;
L=length(x);
z=zeros(L,L);
for nn=1:L
for mm=1:L
R=sqrt(x(nn)^2+y(mm)^2);
z(nn,mm)=sin(R)/R;
end
end
mesh(x,y,z)
hidden off
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :

مثال :
مثال خود نرم افزار متلب :
ابتدا با hidden on ، یک شکل را رسم می کنیم :
close all
clc
mesh(peaks)
colormap hsv
نتیجه :

اکنون همان مثال را با hidden off می نویسیم :
close all
clc
mesh(peaks)
colormap hsv
hidden off
نتیجه :

ساخت ماتریس دو بعدی برای رسم شکل های سه بعدی ، با دستور meshgrid در متلب :
فرض کنید بخواهیم ماتریس z را به صورت یک ماتریس دو بعدی، بر حسب مقادیر مختلف x و y ، تعریف کنیم و سپس آن را به صورت یک شکل سه بعدی (با هر دستور ترسیم سه بعدی دلخواه) رسم کنیم. برای این منظور، قبل از هر چیز باید بازه لازم برای x و y و همچنین مقادیر انتخاب شده از x و y در این بازه را تعریف کنیم. برای این منظور، می توانیم از دستور meshgrid در متلب استفاده کنیم. به مثال زیر توجه کنید :
مثال :
close all
clc
[x,y] = meshgrid(-4:0.1:4,-3:0.1:3)
z=sqrt(x.^2+y.^2);
mesh(x,y,z)
colorbar
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
نتیجه :
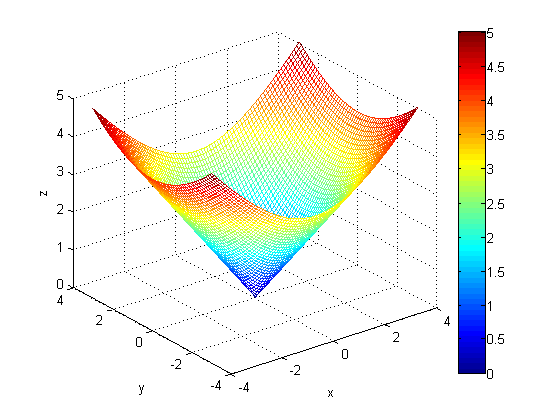
ابتدا با دستور [x,y] = meshgrid(-4:0.1:4,-3:0.1:3) تعیین کرده ایم که بازه تعریفی برای x ، به صورت -4:0.1:4 و بازه تعریفی برای y ، به صورت -3:0.1:3 باشد. سپس مقادیر z را به صورت دلخواه، بر حسب مقادیر مختلف x و y ، به دست آورده ایم. دقت کنید که به کار بردن علامت نقطه (.) بعد از x و y ، ضروری می باشد و معنی آن این است که هر عنصر x یا y ، به توان 2 برسد، نه اینکه کل ماتریس x یا y به توان 2 برسد. سپس ماتریس z را با دستور mesh ، به صورت سه بعدی رسم کرده ایم. دستور colorbar برای این است که مقدار متناظر با رنگ های مختلف، در کنار شکل، نمایش داده شود. دستورات xlabel و ylabel و zlabel ، برای تعیین عنوان برای محورهای مختصات، به کار رفته اند.
ساخت یک تابع مناسب برای تست کردن دستورهای ترسیم ، با دستور peaks در متلب :
دستور peaks در متلب، برای ساخت یک تابع به کار می رود که این تابع معمولا برای تست کردن دستورهای ترسیم در متلب مناسب می باشد. در واقع در میان توابع مختلف، بر حسب تجربه مشخص شده است که دستور peaks ، خیلی خوب می تواند عملکرد دستورات ترسیم مختلف را در متلب نمایش بدهد. البته در سایت کلیدستان، در مباحث آموزش دستورات ترسیم، کمتر از دستور peaks استفاده کرده ایم، زیرا معمولا همه با آن آشنایی ندارند و ممکن است باعث سردرگمی شود. برای آشنایی با شکل حاصل از دستور peaks ، به مثال زیر توجه کنید :
مثال :
close all
clc
[x,y]=meshgrid(-3:0.1:3,-3:0.1:3)
z=peaks(x,y);
mesh(x,y,z)
axis([-3 3 -3 3 -10 5])
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z’)
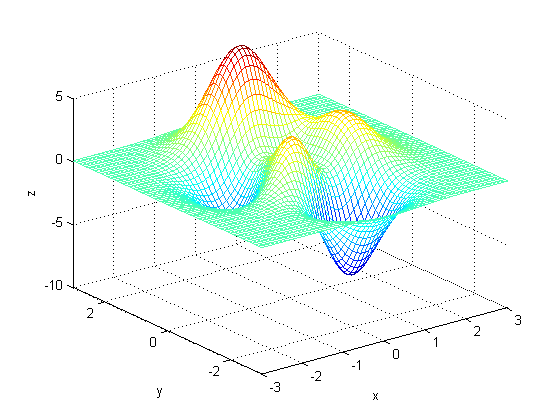
ابتدا با دستور meshgrid ، بازه هایی را برای x و y تعریف کرده ایم. در واقع دستور meshgrid ، برای تعیین مقادیری که با آنها ماتریس دو بعدی z را می سازیم، به کار می رود. سپس دستور peaks برای ساخت تابع مناسبی که گفتیم، استفاده شده است. دستور axis ، برای تعیین محدوده نمایش محورهای مختصات به کار رفته است. دستورات xlabel و ylabel و zlabel نیز برای تعیین عنوان برای محورهای مختصات می باشند.
نتیجه :
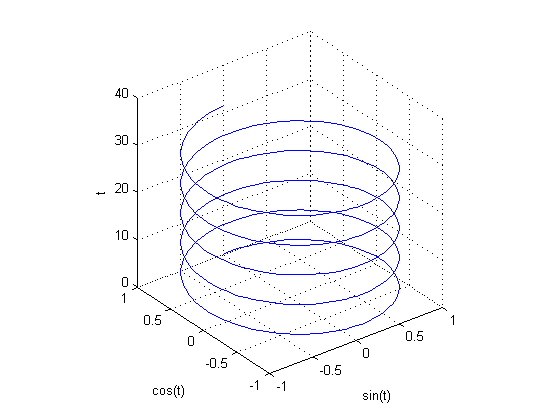
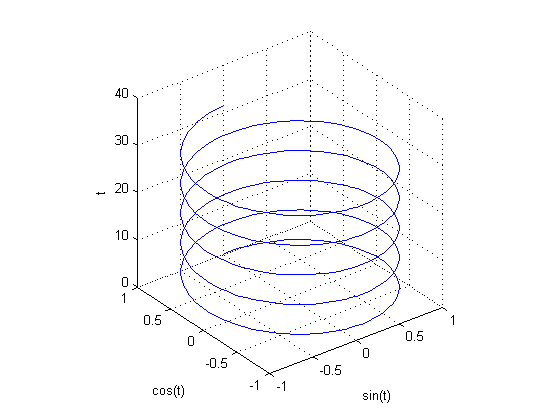
رسم خطوط به صورت سه بعدی با دستور plot3 در متلب :
دستور plot3 در متلب، برای رسم خطوط به صورت سه بعدی به کار می رود. یک مثال مشهور در این زمینه را شرح می دهیم :
مثال :
plot3(sin(t),cos(t),t)
xlabel(‘sin(t)’)
ylabel(‘cos(t)’)
zlabel(‘t’)
grid
axis square
نتیجه :
دقت شود که محور عمودی، برای متغیر t خواهد بود و دو محور افقی نیز به صورت دو تابع از متغیر t می باشند. دستورات xlabel و ylabel و zlabel ، برای تعیین عنوان برای محورهای مختصات می باشند. دستور grid نیز باعث می شود که مقیاس ها، بر روی دیواره های پشت شکل، نمایش داده شوند تا سه بعدی بودن شکل، به خوبی نمایش داده شود. دستور axis square نیز تعیین کرده است که دو محور افقی شکل، با اندازه ای یکسان، نمایش داده شوند که باعث می شود تغییرات دایره ای شکل منحنی، در جهت سطوح افقی، به خوبی مشاهده شود.