تعداد صفحات 13 پرداخت سریع و آسان
خلاصه:
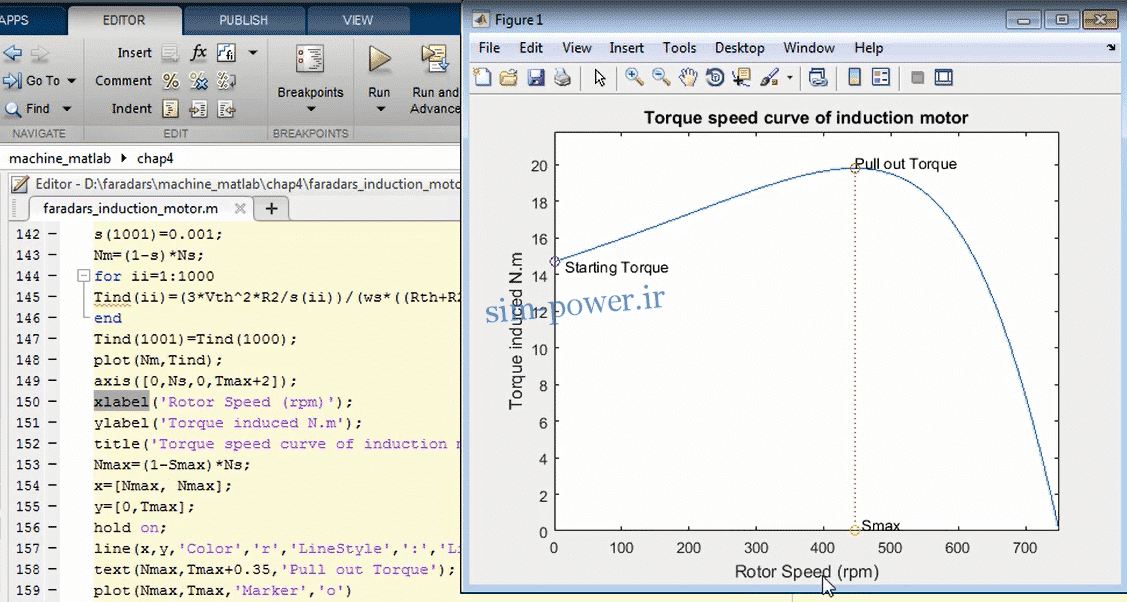
ديناميك شبكه الكتريكي را مي توان با دانستن صفرها و قطبهايش به طور كامل توصيف كرد. هر ترانسفورماتور را مي توان با يك شبكه نردباني كه از حل مدار معادل آن به دست مي آيد بيان كرده و به كمك آن صفرها و قطبهاي تابع انتقال آن را به دست آورد.
ما مي خواهيم يك راه حل كوتاه بر مبناي آناليز فضاي حالت را نشان دهيم. با استفاده از فضاي حالت و توابع لاپلاس شرايط مناسبي براي محاسبه عددي فراهم مي آيد. با استفاده از اين تركيب در عمل ديگر محدوديتي براي سايز شبكه و توپولوژي مدار كه شامل مقاومتها و خازنها و القاگرها است نداريم.
معرفي: ترانسفورماتورهاي HV را عموما براي مقاومت در برابر over voltageها و نيروي مدار كوتاه طراحي مي كنند وقوع اين پديده ها طبيعي و گريز ناپذير است و علت عمده خرابي هاي ترانسفورماتور است. تشخيص به موقع براي جلوگيري از خرابي ها بسيار مهم است براي رسيدن به اين مهم تستهاي تشخيص و condition montoring روشهايي است كه به ما كمك مي كند تا از وقوع خطاها آگاه شويم.
- اگر چه نرم افزارهاي براي آناليز مدار را مي توانيم مورد استفاده قرار دهيم اما آنها فقط شماتيكي از نتيجه TF را نشان مي دهند و اطلاعات كافي درباره قطب وصفر به ما نمي دهند . زيرا در اين نرم افزارهاي تمايز بين دو قطب نزديك به هم و يا جفت صفر و قطب نزديك به هم ( حذف صفر و قطب ) را بسيارمشكل مي توان تشخيص داد.
- در اواسط دهه 1950 يك روش از سوي ABETTI [4] پيشنهاد شد و او از آناليز گره اي براي آناليز مدار معادل يك سيستم كه شامل سيم پيچي دو كوپله بودند استفاده كرد كه فقط براي تعيين فركانس هاي طبيعي مدارهاي سايز كوچك مورد استفاده قرار گرفت .
- در سال 1964، Guruaij [5] متد پاسخ توسعه يافته را ارائه كرد كه بر مبناي راهكار مقادير ويژه بود. اين روش به ما در به دست آوردن فركانسهاي طبيعي و توزيع ولتاژ كمك مي كند و مورد استفاده براي شبكه هاي بزرگ است.
- در سال 1977 و Degene ff [6] يك روش مشابه كه از ماتريس گره اي ادميتانس بود ارائه داد يكي از شرايط آن بدين صورت است كه اتلاف را در نظر نگيريم.
5) FERGETAD [7] در سال 1974 يك راهكار برمبناي فرمول فضاي حالت براي محاسبه نوسانات ارائه داد در اين روش قطب ها مستقيما از مقادير ويژه سيتم و صفرها از معكوس سيستم بدست مي آمد كه روش سر راستي نيست.
III .محاسبه تابع تبديل به كمك فضاي حالت:
روش متغير حالت يك روش بسيار كارآمد براي توصيف رفتار ديناميك يك سيستم يا شبكه روش متغير حالت است KUH وRohrer [8] كارهايي روي آن براي تحليل شبكه انجام داده اند و نتايج را اعلام كرده اند . فضاي حالت برروي سيستم غير خطي متغير با زمان مانند سيستم جايي كه روشهاي كلاسيك از توصيف آن عاجز بودند گسترش يافته است (1)
به طوري كه كيفيت رفتارسيستم،پسيويته، با زمان خطي ، پايداري و … به راحتي با مشخصات متغير حالت قابل بيان است. از مزاياي ديگر اين روش،سيستم با معادله ديفرانسيل مرتبه اول توصيف مي شود و برروي برنامه نويسي بر روي كامپيوتر هاي ديجيتال مناسب است .
A تعريف ها.
حالت يك سيستم بايد اطلاعات كاملي از ديناميك سيستم به ما بدهد يك انتخاب مناسب برروي متغيرهاي حالت آن است كه مجموعه اي معادلات ديفرانسيل خطي مرتبه اول كه از هم مستقل هستند را انتخاب كنيم.
[9] .
عمومي شكل كه براي معادلات خطي lti بيان مي شود
X : متغيرهاي حالت
: مشتق زماني متغيرهاي حالت
U : بردار ورودي
Y بردار خروجي
(A,B.C,D) :ماتريس هاي ثابت هستند
B: انتخاب متغير حالت
براي يك سيستم كه مورد آناليز قرار مي گيرد انتخاب متغيرهاي حالت يكتا نيست . انتخاب تصادفي متغيرهاي حالت ممكن است پيچيدگي را افزايش دهد. براي اجتناب ازاين حالت ها ، راهنمايي هايي براي انتخاب متغير حالت وجود دارد .
متغيرهاي حالت معمولاً با كمك المان هاي ذخيره كننده انرژي تعيين مي شوند در واقع ما به تعداد المان هاي مستقل در يك شبكه متغير حالت كمتري داريم به طور مثال در شكل (1) تعداد متغيرهاي حالت كمتر از عناصر ذخيره كننده انرژي است [10]. بر پايه اين مدل جريان هاي اندوكتانس ها و ولتاژ خازن ها را به عنوان متغيرهاي حالت مطلوب در نظر مي گيريم . به عنوان مثال در يك سيستم به كمك گراف ، گره ها را مشخص مي كنيم درختي كه از عناصر ذخيره كننده تشكيل ميدهد و از همه گرهها ميگذرد را ميتوان به عنوان متغير حالت در نظر گرفت
تعداد صفحات 13 پرداخت سریع و آسان