توزیعهای احتمال و تولید اعداد تصادفی-2

توزیعهای احتمال و تولید اعداد تصادفی

توزیع برنولی (‘bern’)

اگر آزمایش دو برآمد داشته باشد “پیروزی” و “شکست” و احتمال آنها به ترتیب θ و θ – 1 باشد آنگاه تعداد پیروزیها یعنی 0 یا 1 ، توزیع برنولی دارد و بصورت نمادی زیر نمایش داده می‌شود:

1 یا 0=xf(x;θ) = θx(1-θ)1 – x

میانگین و واریانس توزیع برنولی به ترتیب θ و θ-1) θ) می‌باشد.

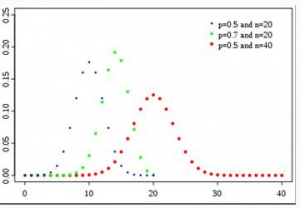
توزیع دوجمله‌ای

احتمال مطلوب برای “x پیروزی در n امتحان” توسط توزیع دو جمله‌ای تأمین می‌گردد که احتمال آن بصورت زیر بدست می‌آید:

میانگین و واریانس توزیع دوجمله ای به ترتیب θn و θ-1)θn) است.

توزیع پواسون (‘po’)

در توزیع دوجمله‌ای هرگاه n بزرگ باشد و θ به سمت صفر میل کند احتمال x پیروزی در n امتحان به توزیع پواسون با پارامتر λ میل می کند که در آن λ=nθ است. میانگین و واریانس توزیع پواسون هر دو با λ برابر است. گر چه توزیع پواسون بصورت شکل حدی توزیع دوجمله‌ای حاصل شده است، ولی کاربردهای فراوانی دارد که شاید در بسیاری از مواقع رابطه مستقیمی با توزیع دوجمله‌ای نداشته باشد. مثلا توزیع پواسون را می‌توان به عنوان مدلی برای تعداد پیروزیهایی که در طول فاصله زمانی مفروض یا در ناحیه مشخصی رخ می‌دهند به کاربرد به شرط آنکه:

1- تعداد پیروزیها در فاصله زمانی یا در ناحیه‌های نامتداخل مستقل باشند.

2- احتمال رخ داد تنها یک پیروزی در هر فاصله زمانی کوتاه یا در هر ناحیه کوچک متناسب با طول فاصله زمانی یا اندازه ناحیه باشد.

3- احتمال رخداد بیش از یک پیروزی در چنین فاصله زمانی کوتاه یا قرار گرفتن در چنین ناحیه ای کوچک ، ناچیز باشد. بنابراین توزیع پواسون می تواند تعداد مطالعات تلفنی اداره ای را در یک ساعت مشخصی ، تعداد خطاهای تایپی را در یک صفحه و … را به ما بدهد.

توزیع نمایی (‘exp’)

برای پیدا کردن تعداد پیروزیها در فاصله زمانی مفروض برای متغیر تصادفی X از توزیع پواسون استفاده کردیم. توزیع نمایی چگالی احتمال متغیر تصادفی پیوسته y است که زمان انتظار تا اولین پیروزی را به ما می دهد در این صورت توزیع نمایی با فرض λ=1/θ یا λ=α به شکل زیر در می‌آید:

توزیع نرمال (‘norm’)

متغیر تصادفی X دارای توزیع نرمال است اگر و تنها اگر چگالی احتمال آن بصورت زیر باشد:

در تعریف فوق هرگاه 0=μ و 1=σ باشد توزیع نرمال استاندارد نامیده می شود. در توزیع دوجمله‌ای وقتی n ، تعداد امتحانها ، خیلی بزرگ باشد و θ ، احتمال پیروزی در یک تک امتحان نزدیک 2/1 باشد با توزیع نرمال تقریب می‌خورد. با افزایش n این تقریب بهتر خواهد شد. برای توزیع نرمال می‌توان گفت اگر X دارای توزبع نرمال با میانگین μ و انحراف معیار σ باشد، آنگاه نرمال استاندارد است.

 

 

نوعی توزیع پر مصرف در آمار، اقتصاد، و علوم تجربی است.

یک آزمایش دوجمله‌ای بایستی دارای ویژگیهای زیر باشد[۱]:

آزمایش دارای n تعداد آزمون یکسان و عینا مشابه باشد.

نتیجه هر آزمون به یکی از فقط دو صورت باشد: موفق یا ناموفق

احتمال موفقیت آزمونی را اگر با p نشان دهیم، از آزمون به آزمون یکسان بوده و متغیر نباشد. احتمال ناموفقیت را با q نشان داده که برابر است با

‎1-p

آزمونها مستقل باشند.

متغیر تصادفی Y نام دارد، که تعداد موفقیتهای n آزمون را نشانگر است.

علاوه بر این، باید توجه داشت که اگر حجم نمونه قابل قیاس با حجم جامعه باشد، استفاده از توزیع هایپرژئومتریک را باید در نظر گرفت.

مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,