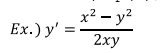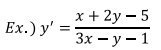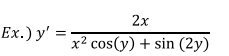میدان برداری گرادیان و حل معادلات دیفرانسیل در متلب

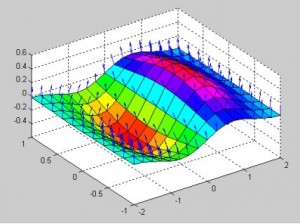
مثال از میدان برداری گرادیان

>[X,Y] = meshgrid(-2:0.25:2,-1:0.2:1);
>>Z = X.* exp(-X.^2 – Y.^2);
>>[U,V,W] = surfnorm(X,Y,Z);
>>quiver3(X,Y,Z,U,V,W,0.5);
>>hold on
>>surf(X,Y,Z);
>>colormap hsv
>>view(-35,45)
>>axis ([-2 2 -1 1 -.6 .6])
>>hold off

ترسيم پارامتريك سطوح

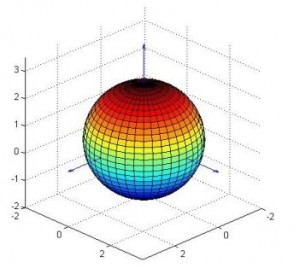
مثال) ميخواهيم كره اي با مختصات زير رسم كنيم :

> a=2;
>> u=linspace(0,2*pi,41);
>> v=linspace(-pi/2,pi/2,31);
>> [U,V]=meshgrid(u,v);
>> X=a*cos(V).*cos(U);
>> Y=a*cos(V).*sin(U);
>> Z=a*sin(V);
>> surf(X,Y,Z)
>> axis image

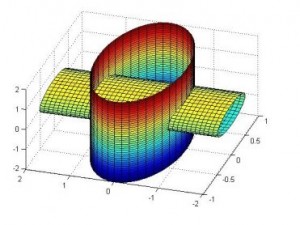
مثال) نمايش تقاطع دو استوانه

>> u=linspace(0,2*pi,41);
>> v=linspace(-2,2,41);
>> [U,V]=meshgrid(u,v);
>> %vertical cylinder with r=1
>> surf(cos(U),sin(U),V)
>> hold on
>> %horizental cylinder with r=5
>> surf(0.5*cos(U),V,0.5*sin(U))
>> hold off

استفاده از فرمان ezsurf براي ترسيم سطوح پارامتريو a<s<b كه باشند مي t و s پارامترها .باشد مي ezsurf(x,y,z,[a b c d]) صورت به فرمان ايناست. c<t<d
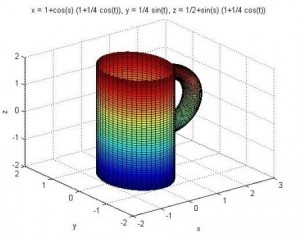
مثال) ترسيم يك ليوان :

> syms s t
>> %vertical cylinder with r=1
>> x=cos(s);
>> y=sin(s);
>> z=t;
>> ezsurf(x,y,z,[0 2*pi -2 2])
>> hold on
>> %handle r=1 centered in (1,0,0.5)
>> xhandle=1+cos(s)*(1+0.25*cos(t));
>> yhandle=0.25*sin(t);
>> zhandle=0.5+sin(s)*(1+0.25*cos(t));
>> ezsurf(xhandle,yhandle,zhandle,[-pi/2 pi/2 0 2*pi])
>> hold off
>> axis([-2 3 -2 2 -2 2])

معادلات ديفرانسيل مرتبه اول

هرچند که MATLAB يک نرم افزار مخصوص مسايل آناليز عددي مي باشد ولي قادر است مسايل مربوط به معادلاتديفرانسيل را به طور نمادين حل نمايد. به عنوان مثال مي خواهيم معادله ديفرانسيل را حل کنيم.

تذکر: مشتقات y را بايد به صورت اپراتور وارد نمود.
تابع مورد استفاده در اين مبحث، ()dsolve مي باشد که مخصوص حل نمادين معادلات مي باشد.

مثال مطرح شده را اين گونه حل مي کنيم :

> syms x y
>> y=dsolve(‘Dy=y*x’,’x’)
y =
C1*exp(1/2*x^2)

حل معادلات ديفرانسيل با شرايط مرزي

کافي است شرايط مرزي را در تابع dsolve وارد نماييم.

>> syms x y
>> y=dsolve(‘Dy=y*x’,’y(1)=1′,’x’)
y =
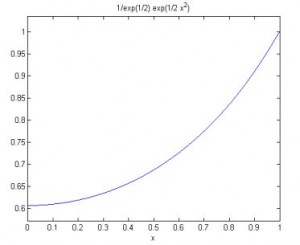
1/exp(1/2)*exp(1/2*x^2)

حالا مي خواهيم تابع y که در بالا به دست آمد را در بازه [0,1] رسم کنيم :

>> ezplot(y,[0 1])

– براي آشنايي بيشتربه حل چند معادله مي پردازيم :

> syms xy
>> y=dsolve(‘Dy=1+x+y^2+x*y^2′,’x’)
y =

tan(x+1/2*x^2+C1)

> syms xy
>> y=dsolve(‘Dy=tan(x+y)-1′,’x’)
y =
-x+asin(exp(x)/C1)

> syms xy
>> y=dsolve(‘Dy=(x^2-y^2)/(2*x*y)’,’x’)
y =
1/3/x*3^(1/2)*(x*(x^3+3*C1))^(1/2)
-1/3/x*3^(1/2)*(x*(x^3+3*C1))^(1/2)

> syms xy
>> y=dsolve(‘Dy=(x+2*y-5)/(3*x-y-1)’,’x’)
y =
-1/2*log(((-1+x)^2+(-y+2)*(-1+x)+(-y+2)^2)/(-1+x)^2)-
5/3*3^(1/2)*atan(1/3*(3+x-2*y)*3^(1/2)/(-1+x))-log(-1+x)-C1 =
0

تذکر: در تمامي موارد بالا بعد از حل معادله براي نمايش بهتر y مي توان دستور (pretty(y<< را اجرا نمود.

> syms xy
>> y=dsolve(‘x*(Dy)-3*y=x^2′,’x’)
y =
(-1+C1*x)*x^2

> syms x y
>> y=dsolve(‘Dy-y=x*y^2′,’x’)
y =
-1/(-1+x-exp(-x)*C1)

> syms x y
>> y=dsolve(‘Dy=(2*x)/(x^2*cos(y)+sin(2*y))’,’x’)
y =

-asin(lambertw(-1/2*C1*exp(-1/2*x^2-1))+1/2*x^2+1)

که تابع w لامبرت (Lambert’s W function) به صورت زيرمي باشد :

W = lambertw(X) :

> syms x y
>> y=dsolve(‘Dy=x^3+(2/x)*y-(1/x)*y^2′,’x’)
y =
-i*tan(1/2*i*x^2-C1)*x^2

> syms x y
>> y=dsolve(‘(Dy)*cos(y)+sin(y)=x+1′,’x’)
y =
asin((exp(x)*x-C1)/exp(x))

> syms x y
>> y=dsolve(‘4*x*y+3*y^2-1+(x^2+2*x*y)*(Dy)=0′,’x’)
y =
-1/6*(3*x^3-(9*x^6+12*x^4-36*C1*x)^(1/2))/x^2
-1/6*(3*x^3+(9*x^6+12*x^4-36*C1*x)^(1/2))/x^2

> syms x y
>> y=dsolve(‘(y+log(x))=x*Dy’,’x’)
y =
-log(x)-1+C1*x

> syms x y a
>> y=dsolve(‘Dy=-(x-a)^0.5′,’x’)
y =
-2/3*(x-a)^(3/2)+C1

> syms x y
>> y=dsolve(‘x*y*(Dy)^2+(x^2+x*y+y^2)*(Dy)+x^2+x*y=0′,’x’)
y =
(1/2*5^(1/2)-1/2)*x
(-x^2+C1)^(1/2)

(-1/2*5^(1/2)-1/2)*x
-(-x^2+C1)^(1/2)
(-x^2+C1)^(1/2)

>> syms x y
>> y=dsolve(’16*x^2+2*((Dy)^2)*(y)-((Dy)^3)*x=0′,’x’)
y =
3/2*(-4*x)^(1/3)*x