مثال هاي مكانيك

مثال هاي مكانيك

آناليز پرتابه projectile

پرتابه اي را با زاويه 45 درجه و سرعت اوليه 60 متر بر ثانيه پرتاب ميكنيم. در فاصله زماني بين صفر و 8 ثانيه، مسير پرتابه در فضا،. سرعت پرتابه، و زاويه پرتابه را برحسب زمان رسم كنيد.

% projectile.m echo off;

d0 = 45; v = 60; g = 9.8; % constant values

a = d0 * pi / 180; % convert to radians

t = 0 : 0.1 : 8; x = v * t * cos(a); % horizontal displacement

y = v * t * sin(a) – 0.5 * g * t .^ 2; % vertical displacement

subplot(2,2,1), plot(x,y),xlabel(‘x’),ylabel(‘y’) title(‘Space Path of a Projectile Trajectory’)

vx = v * cos(a); % horizontal velocity

vy = v * sin(a) – g * t; % vertical velocity

V = sqrt( vx^2 + vy.^2 ); % Magnitude of velocity

subplot(2,2,2), plot(t,V,’g’)

xlabel(‘Time’), ylabel(‘Magnitude of Velocity’)

d = 180 / pi * atan2( vy, vx ); % angle at time t

subplot(2,2,3), plot(t,d,’r’)

xlabel(‘Time’),ylabel(‘Angle of Projectile’)

>> projectile

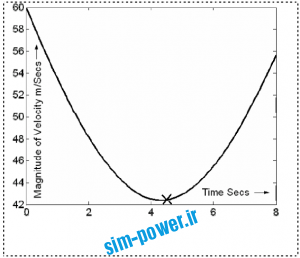
سرعت پرتابه و يافتن مينيمم آن

ام- فايلي با نام trj.m بنويسيد كه: الف) بزرگاي سرعت يك پرتابه را با نخستينه هاي: زاويه پرتاب d0 = 45، سرعت اوليه v = 60، و شتاب گرانش g = 9.8 در فاصله زماني 0 : 0.1 : 8 رسم كند. روي مينيمم سرعت علامت × بزنيد. ب) مقادير مينيمم و ميانگين منحني را با استفاده از پنجره Data Statistics نشان دهيد.

% trj.m v = 60;

g = 9.8;

d0 = 45; t = 0 : 0.1 : 8;

a = d0 * pi / 180;      % converts to radians

vx = v * cos(a);

vy = v * sin(a) – g * t;

V = sqrt( vx^2 + vy.^2 );

plot(t,V,’g’)

xlabel(‘Time Secs’)

ylabel …

‘Magnitude of Velocity m/s’

k = find(V == min(V));

hold on,

plot(t(k),V(k),’x’) %

V(k) is min(V) hold off

عبارت ((k = find(V == min(V انديس نقطه مينيمم را پيدا ميكند.

مثال هاي الكتريكي

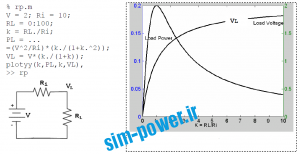
توان مصرفي مقاومت در شكل 8-6 با داشتن k ، توان مصرفي، ولتاژ بار، و توان اتصال كوتاه باطري اينگونه نوشته ميشوند.

توان مصرفي و ولتاژ بار را برحسب k (كه نمايش مقدار بار است) رسم كنيد. V = 12, Ri = 10

 

مدار معادل چند مقاومت موازي

مقاومت معادل سه مقاومت موازي R1 = 15, R2 = 25, R3 = 80 را پيدا كنيد.

% resi.m

RR = [15 25 80];

n1 = ones(1,3) % creates a vector of three ones

RI = n1./RR; % reverses all three elementds of RR

disp([‘RI = ‘ num2str(RI)]);

SRI = sum(RI); % sums up the reverse elements

RT = 1/SRI; % gives the equivalent resistance of three

disp([‘RT = ‘ num2str(RT)]);

>> resi

n1 = 1.00 1.00 1.00

RI = 0.066667 0.04 0.0125

RT = 8.3916

نویسنده: مصطفی همت آبادی

 

مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,