نمودارهاي ٢ بعدي در متلب

نمودارهاي ٢ بعدي در متلب
مجموعه دستورات زير نحوه ترسيم يك تابع بر حسب يك متغير مستقل را نشان مي دهد:

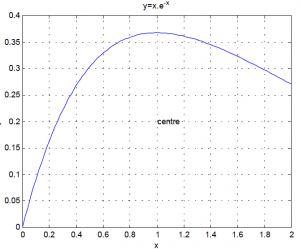
» x=linspace(0,2); y=x.*exp(-x);
» plot(x,y)
» grid
» xlabel(‘x’)
» ylabel(‘y’)
» title(‘y=x.e^{-x}’)
» text(1,.2,’centre’)

 

هفت خط فوق به ترتيب اعمال زير را انجام مي دهند:
١- بردار متغيرهاي مستقل (x) و تابع (y) را ايجاد مي كند.
٢- مقادير y را بر حسب x رسم مي نمايد.
٣- شبكه را به نمودار مي افزايد.
٤- توضيح محور افقي را مي نويسد.
٥- توضيح محور عمودي را مي نويسد.
٦- تيتر نمودار را در بالاي آن مي نويسد.
٧- در نقطه مورد نظر (در اين مثال نقطه ( 0.2 و 1))  متغير حرفي مشخص شده (در اين مثال centre) را مي نويسد.

مي توانيد نمودار ايجاد شده را به كمك دستور Save As در منوي File پنجره نمودار، ذخيره نماييد. اين دستور نمودار را در يك پرونده كه نام آن را خودتان وارد خواهيد كرد و دنباله آن ffig. مي باشد ذخيره مي كند. شما مي توانيد اين نمودار را در دفعات بعدي كار با MATLAB بازيابي نماييد. با استفاده از دستور open در هنگام رسم نمودارها مي توانيد از علامتهاي مختلف (بجاي خط) براي رسم توابع استفاده كنيد.

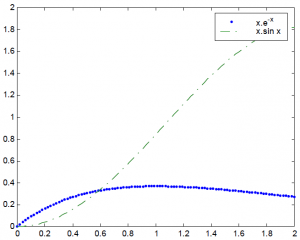
همچنين مي توانيد بيش از يك تابع را در يك نمودار نمايش دهيد.

» plot(x,y,’.’,x,x.*sin(x),’-.’)

و در صورت لزوم نام توابع را نيز در همان نمودار نشان دهيد.

» legend(‘x.e^{-x}’,’x.sin x’)

 

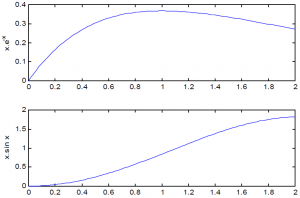
مي توانيد بيش از يك نمودار را در يك پنجره نشان دهيد:

» subplot(2,1,1), plot(x,y)
» ylabel(‘x.e^{-x}’)
» subplot(2,1,2), plot(x,x.*sin(x))
» ylabel(‘x.sin x’)

دو عدد اول در دستور subplot تعداد تقسيمات صفحه را معين مي كنند (سطري و ستوني) و عدد سوم مكان رسم نمودار (يا تغيير روي نمودار موجود) را مشخص مي نمايد.
مي توانيد با استفاده از دستور clf نمودار را پاك كنيد.

» clf

با استفاده از دستور figure مي توانيد پنجره جديدي براي رسم نمودار باز نمائيد. دستور axis حدود بالا وپايين محورهاي مختصات را به صورت يك بردار ارائه مي نمايد.

» figure(2)
» plot(x,y)
» axis
ans =
0 2.0000 0 0.4000
0

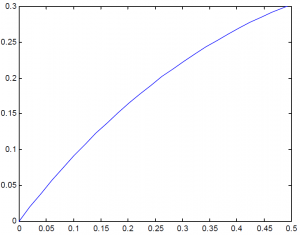
در تمامي مثالهاي بالا مقادير متغير مستقل و متغير وابسته به صورت دو بردار بر حسب هم رسم شده اند. در صورتي كه تابعيت متغير وابسته بر حسب متغير مستقل مشخص باشد مي توانيد از دستور fplot براي رسم آن استفاده كنيد:

» fplot(‘x*exp(-x)’,[0 2])

آرگومان اول اين دستور يك بردار حرفي است كه مشخص كننده رابطه تابع (در صورت ساده بودن رابطه تحليلي تابع، همانند مثال فوق) يا نام m-file حاوي تابع (كه جداگانه بايد ايجاد شده باشد) است. آرگومان دوم fplot يك بردار دو عضوي است كه حد پائين و بالاي متغير مستقل را مشخص مي كند.

تعدادي از دستورهاي ترسيم دو بعدي در زير آورده شده اند:

نمودار نيمه لگاريتمي (محور x لگاریتمی)                          (semilogx(x,y

نمودار نيمه لگاريتمي (محور y لگاریتمی)                          (semilogy(x,y

نمودار تمام لگاريتمي                                                   (loglog(x,y

رسم در دستگاه مختصات قطبي                                     (polar(r,theta

نمودار ميله اي                                                            (bar(x,y

نمودار مساحت                                                           (area(x,y

 

مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,