مشتقات نمایی، لگاریتمی و توابع مثلثاتی
جدول زیر مشتقات نمایی، لگاریتمی و توابع مثلثاتی را به طور معمولی استفاده می کند:
| مشتق | تابع |
| ca.x.ln c.a(در لگاریتم طبیعی) | ca.x |
| ex | ex |
| 1/x | ln x |
| 1/x.ln c | lncx |
| xx.(1+ln x) | xx |
| cos(x) | sin(x) |
| -sin(x) | cos(x) |
| sec2(x), or 1/cos2(x) , or 1+tan2(x) | tan(x) |
| -csc2(x),or -1/sin2(x),or –(1+cot2(x)) | cot(x) |
| sec(x).tan(x) | sec(x) |
| -csc(x).cot(x) | csc(x) |
مثال
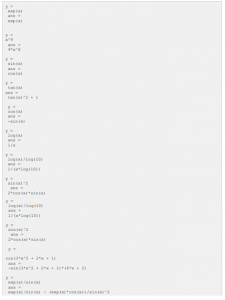
یک فایل اسکریپت ایجاد کنید و کد زیر را در آن تایپ نمایید:
syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = loq(x)
diff(y)
y = logl0(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2+2*x +1)
diff(y)
y = exp(x) / sin(x)
diff(y)
زمانی که فایل را ایجاد می کنید، نتیجه زیر نشان داده می شود:
در زیر معادله octave از محاسبات بالا است:
pkg load symbolic
symbols
x = sym(“x”):
y =exp (x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y =sih(x)
differentiate(y,x)
y =tan(x)
differehtiate(y,x)
y =cos(x)
differentiate(y,x)
y =log(x)
differentiate(y,x)
% symbolic packages does hot have this support
%y =logl0(x)
%differentiate(y,x)
y =sih(x)a2
differentiate(y,x)
y =cos(3*xa2+2*x +1)
differentiate(y,x)
y =exp(x)/sih(x)
differentiate(y,x)
نویسنده: مهندس عربعامری
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,