ساختارهاي تكرار
حلقه for
در اين حلقه شمارندهاي index از مقدار اوليه تا مقدار نهائي خود را با گام معين طي ميكند، و حلقه براي هر گام تغييرِ شمارنده تكرار ميشود. ميتوان شمارنده را مساوي يك بردار قرار داد. مثال ها:
جدول توان
% fr.m d = 1:2:9; for k = d disp(k^2)
end
>> fr
1 9 25 49 81
جدول سينوس، كسينوس
% sn.m
v = [0 : pi/6 : pi];
fprintf(‘\n’);
disp([‘Angle Sine Cosine’])
for k = v
fprintf(‘%6.2f %6.2f %6.2f\n’,180*k/pi, sin(k), cos(k));
end
>> sn
Angle Sine Cosine
0.00 0.00 1.00
30.00 0.50 0.87
60.00 0.87 0.50
90.00 1.00 0.00
120.00 0.87 -0.50
150.00 0.50 -0.87
180.00 0.00 -1.00
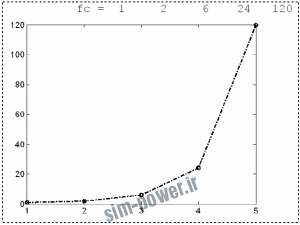
تعييين فاكتوريل عدد صحيح مثبت، اعداد 1 تا 5
% fac.m
clear متغيرها را از حافظه پاك ميكند %
n = 5; fact = 1; ss = 1;
for k = ss : n
fact = k*fact;
fc(k) = fact;
end
fc plot([ss:n],fc,’Or’)
>> fac 1
بلوك try…catch
مثال:
اعضاي يك ماتريس سلولي را جداگانه چاپ كنيد. وقتي به آخر رسيد برنامه تمام وپيغام Not Found ديده شود.
%TryCth.m
echo off
n=1:10;
A={‘Number’ 234 ‘next’ 9} ;
for k=n
try
disp(A(k)) catch disp(‘Not Found’), break end end
>> TryCth.m
به دست آوردن طول زمان محاسبه حاصلجمع اعداد بين صفر تا يك بيليون با گام صد
يك شمارنده است با مقدار نهائي يك بيليون با گام صد
t0 = clock; s1 = 0;
% for n = 0 : 100 : 1e9
s1 = s1 + n ;
end
elaps1 = num2str(etime(clock,t0));
disp( [‘For loop duration = ‘, elaps1, ‘ Secs’])
disp([‘sum1 = ‘ num2str(s1)])
تابع ()etime فاصله زماني بين آرگومانهايش را ميدهد، براي آوردن در disp به رشته تبديل شده است.
بردار به جاي حلقه for
مثال فوق را بدون استفاده از for حل كنيد. طول زمان اين دو روش را براي كامپيوتر خودتان مقايسه كنيد.
t0 = clock;
m = 0 : 100 : 1e9;
s2 = sum(m);
elaps2 = num2str(etime(clock,t0));
disp( [‘Vectorization duration = ‘, elaps2 ‘, Secs’])
disp([‘sum2 = ‘ num2str(s2)])
در بعضي موارد استفاده از حلقه for الزامي است و نميتوان به جاي حلقه for از بردار استفاده كرد.
حلقه while و دستور break
حلقه while مانند for دستورات داخل حلقه را تكرار ميكند، اما شمارنده ندارد. دستورات داخل حلقه while تازمانيكه شرط مقابل كلمه while برقرار باشد اجرا خواهند شد.
مثال: تعيين اعداد اول
يك M-File بهنام primen.m بنويسيد كه اعداد اول كوچكتر از n >= 5) n)را به دست آورد.
اين مثال كاربردهاي عبارات و توابع زير را نيز توضيح ميدهد. به توضيحات توجه شود:
input(), fprintf(), while, for, if, break, end, rem() % primen.m n = input(‘Enter upper limit: ‘);
برنامه، 2 و 3 را محاسبه نميكند لذا آنها را جدا چاپ ميكنيم
% ;(fprintf(‘%d %d’,2,3 ii = 5;
از 5 شروع ميكنيم و تقسيم پذيري ii بر كليه اعداد ماقبلش را امتحان ميكنيم تا نهايتاٌ ii به n برسد
% while ii < n for jj = 2 : ii-1 if rem(ii,jj)== 0 % break
اگر تقسيم پذير بود عدد، اول نيست و برنامه به عبارت ii=ii+1 ميرود %
end
if jj == fix(sqrt(ii))
اگر jj تا ريشه دوم ii بالا بيايد و مقسوم عليه آن نباشد، عدد، اول است و چاپ ميشود %
fprintf(‘ %d’,ii);
break
end
end
ii = ii + 2;
% excludes odd numbers end
>> primen
نویسنده: مصطفی همت آبادی
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,