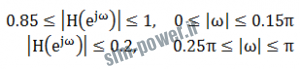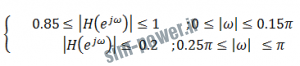خرید پروژه فيلتر dsp
هدف طراحی یک فیلتر فرکانس‌گزین گسسته در زمان با مشخصات داده‌شده است. برای این منظور مراحل زیر را انجام دهید:
- با استفاده از روال طراحی و نیز روابط مربوطه، فیلتر با مشخصات مورد نظر را طراحی کنید. این مرحله شامل موارد زیر است:
- فیلتر IIR
- پارامترهای فیلتر پیوسته در زمان نمونه؛ شامل درجه فیلتر (N)، فرکانس قطع (
) و پارامتر تموج (
) را تعیین کنید. - تابع تبدیل فیلتر پیوسته در زمان نمونه را به دست آورید. این کار شامل یافتن قطب‌های تابع تبدیل است.
- تابع تبدیل فیلتر گسسته در زمان را به دست آورید. این مرحله شامل تجزیه تابع تبدیل فیلتر پیوسته در زمان نمونه به کسرهای جزئی و سپس یافتن تابع تبدیل فیلتر گسسته در زمان مطلوب مطابق روال معرفی‌شده است.
توجه: تمام موارد فوق باید با استفاده از روال طراحی و روابط معرفی‌شده در درس و به صورت تحلیلی انجام شوند. برای اطمینان از درستی طراحی، پارامترهای مربوطه را با استفاده از دستورهای آماده موجود در MATLAB هم به دست آورید.
- فیلتر FIR
- پارامترهای طول (M) و شکل () پنجره Kaiser مناسب را تعیین کنید. این کار باید با استفاده از روال طراحی و روابط معرفی‌شده در درس و به صورت تحلیلی انجام شود. برای اطمینان از درستی طراحی، پارامترهای مربوطه را با استفاده از دستورهای آماده موجود در MATLAB هم به دست آورید.
- به منظور مقایسه، پارامتر طول پنجره Hamming مناسب را هم به دست بیاورید.
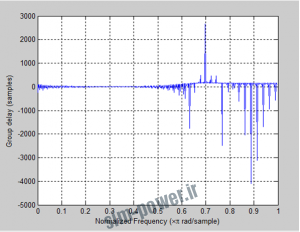
- پاسخ ضربه، پاسخ دامنه، پاسخ لوگاریتم دامنه و پاسخ تأخیر گروه فیلتر (یا فیلترهای) حاصل را رسم کنید.
- آزمایش‌های زیر بر روی فیلتر طراحی‌شده انجام دهید:
- با اعمال یک ورودی سینوسی (تک‌فرکانس) در باندهای مختلف، عملکرد فیلتر را بررسی کنید. برای این منظور فرکانس سیگنال ورودی را یک بار در باند (یا باندهای) عبور فیلتر انتخاب کرده و بار دیگر در باند (یا باندهای) قطع فیلتر
- با اعمال یک سیگنال نویز سفید به ورودی عملکرد فیلتر را بررسی کنید. توجه کنید که نویز سفید، یک سیگنال تصادفی غیرهمبسته است، لذا چگالی طیفی آن در همه فرکانس‌ها یکسان است. بنابراین انتظار داریم که چگالی طیفی سیگنال خروجی فیلتر مطابق با پاسخ دامنه فیلتر باشد.
- یک گزارش مختصر، جامع و مفید از پروژه تهیه کنید که علاوه بر شرح مراحل طراحی تحلیلی و روابط مربوطه، شامل نمودارهای پاسخ ضربه، پاسخ دامنه، پاسخ لوگاریتم دامنه و پاسخ تأخیر گروه فیلتر و نیز نتایج آزمایش‌های انجام‌شده باشد.
طراحی یک فیلتر پایین‌گذر IIR با مشخصات زیر:
با تقریب Butterworth با استفاده از روش Impulse Invariance
طراحی یک فیلتر میان‌گذر FIR با مشخصات زیر:
به روش پنجره کردن
فیلتری با مشخصات زیر :
می دانیم که در فیلتر باترورث: 
، در نظر می گیریم : پس خواهیم داشت:
چون در روش Impulse Invariance 
است.
با جایگذاری دو فرکانس 
در رابطه مربع اندازه و در نظر گرفتن این که اندازه در باند عبور باید از 0.85 بیش تر و در باند توفق از 0.2 کم تر باشد داریم:
و برای محاسبه ی 
از یکی از شروط یاد شده ی باند عبور یا باند توقف استفاده می کنیم، اگر از شرط باند عبور استفاده کنیم رابطه زیر را خواهیم داشت :
با محاسبه مقادیر به صورت زیر به دست می آیند:
و در متلب داریم:
که :
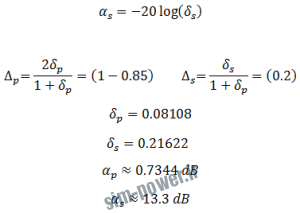
لذا متلب به دست می دهد:
که با تحلیل دستی مطابقت دارند. حال بایستی محل قطب ها و گین را به دست آوریم:
و با داشتن شعاع دایره باترورث قطب ها را به دست می آوریم:2Nبا در نظر گرفتن دایره واحد و تقسیم بندی آن به
,
در متلب :
|
[b,a]=butter(N,Wc,’s’); [b,a] = eqtflength(b,a); [z,p,k] = tf2zp(b,a); |
و نتایج:
|
z = Empty matrix: 0-by-1
p = -0.0585 + 0.1800i -0.0585 – 0.1800i -0.1893 + 0.0000i -0.1531 + 0.1113i -0.1531 – 0.1113i k = 2.4299e-04 |
که با تحلیل دستی مطابقت دارند.
به کسرهای جزئی داریم:H(s)با تجزیه
|
[b,a]=butter(N,Wc,’s’); [r, p, k] = residue(b,a); |
و نتایج:
|
r = 0.3586 + 0.0000i -0.0262 + 0.0805i -0.0262 – 0.0805i -0.1531 – 0.2108i -0.1531 + 0.2108i p = -0.1893 + 0.0000i -0.0585 + 0.1800i -0.0585 – 0.1800i -0.1531 + 0.1113i -0.1531 – 0.1113i k = [] |
که با تحلیل دستی مطابقت دارند.
می دانیم که در روش تغییر ناپذیری پاسخ ضربه داریم:
با داشتن این رابطه تابع انتقال گسسته به صورت زیر حاصل می شود:
که:
و در متلب:
|
[num,den]=butter(N,Wc,’s’); [Bz,Az]=impinvar(num,den,1); [A, M, k] = residuez(Bz,Az);
|
نتایج:
|
A = -0.0262 + 0.0805i -0.0262 – 0.0805i -0.1531 – 0.2108i -0.1531 + 0.2108i 0.3586 + 0.0000i M = 0.9279 + 0.1689i 0.9279 – 0.1689i 0.8527 + 0.0953i 0.8527 – 0.0953i 0.8276 + 0.0000i k = 0
|
که با تحلیل دستی مطابقت دارند.
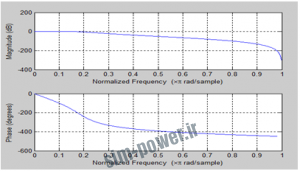
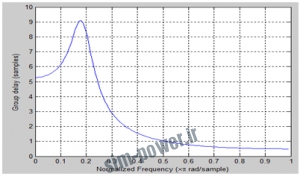
دستورات لازم برای رسم پاسخ فرکانسی :
|
[b,a]=butter(N,Wc); freqz(b,a); figure; grpdelay(b,a,128) |
توجه: تمام نمودارها در بازه 
رسم شده اند.
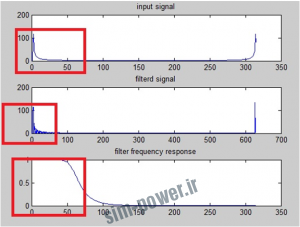
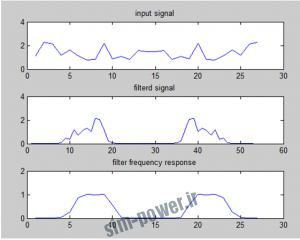
آزمایش موج تک تن سینوسی :
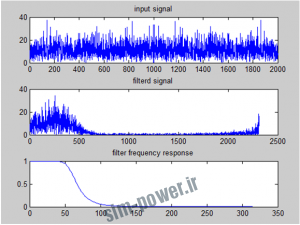
اگر طیف ورودی در باند عبور باشد فیلتر آن را عبور می دهد:
اگر طیف ورودی در باند عبور باشد فیلتر آن را تضعیف می کند :
|
[H,W] = freqz(b,a,n); n=0:0.01:pi; x=cos(3*n); %signal resides within the pass band. x=cos(1000*n); %signal resides outside the pass band. h=ifft(H); X=fft(x); y=conv(x,h); Y=fft(y); figure; subplot(3,1,1);plot(abs(X));title(‘input signal’); subplot(3,1,2);plot(abs(Y));title(‘filterd signal’); subplot(3,1,3);plot(abs(H));title(‘filter frequency response’); |
آزمایش نویز سفید:
چگالی طیفی نویز سفید در همه فرکانس‌ها یکسان است. بنابراین چگالی طیفی سیگنال خروجی فیلترشده هم شکل با پاسخ دامنه فیلتر است.
دستورات متلب مربوطه :
|
[H,W] = freqz(b,a,n); x=rand(2000,1)-0.5; X=fft(x); y=conv(x,h); Y=fft(y); figure; subplot(3,1,1);plot(abs(X));title(‘input signal’); subplot(3,1,2);plot(abs(Y));title(‘filterd signal’); subplot(3,1,3);plot(abs(H));title(‘filter frequency response’); |
طراحی فیلترFIR:
فیلتری با مشخصات زیر :
در روش پنجرهKaiser داریم:
و نیز می دانیم که :
لذا
در متلب داریم که :
ابتدا فرکانس نمونه برداری را برابر 
فرض می کنیم.
دستورات متلب مربوطه :
|
fsamp = 8000; fcuts = [1000 1600 2400 3000]; mags = [0 1 0]; devs = [0.02 0.02 0.02]; [n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp); n = n + rem(n,2); h = fir1(n,Wn,ftype,kaiser(n+1,beta),’noscale’); |
به ترتیب از جپ به راست فرکانس های قطع فیلتر میان گذر مربوطه را می دهند، مثلا fcuts فرکانس های داخل بردار
فرکانس 2400 به این صورت محاسبه شده است:
مقادیر اعوجاج در باندهای قطع پایین ، عبور و قطع بالا را می دهند که همگی 0.02 هستند.devs بردار
با اعمال دستورات بدست می آوریم :
|
n = 25 beta = 2.6523 |
است.)M همان طول فیلتر یا nکه با تحلیل دستی مطابقت دارند.(
رسم پاسخ فرکانسی :
|
freqz(h); |
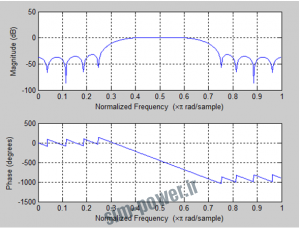
طول پنجرهHammingمعادل
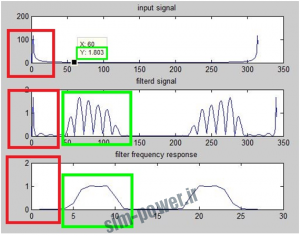
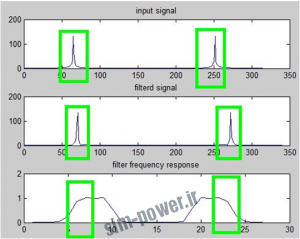
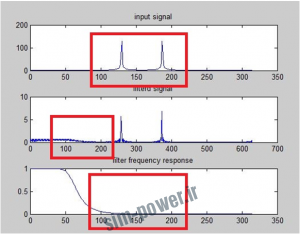
آزمایش موج تک تن سینوسی :
اگر طیف ورودی در باند عبور(میانی ) نباشد فیلتر آن را عبور نمی دهد(مستطیل های قرمز) و گر طیف ورودی در باند عبور(میانی ) باشد فیلتر آن را عبور می دهد(مستطیل های سبز) .
دستورات متلب :
|
fsamp = 8000; fcuts = [1000 1600 2400 3000]; mags = [0 1 0]; devs = [0.02 0.02 0.02]; [n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp); n = n + rem(n,2); h = fir1(n,Wn,ftype,kaiser(n+1,beta),’noscale’); H=fft(h); n=0:0.01:pi; x=cos(3*n); %signal resides outside the pass band. x=cos(500*n); %signal resides within the pass band. X=fft(x); y=conv(x,h); Y=fft(y); figure; subplot(3,1,1);plot(abs(X));title(‘input signal’); subplot(3,1,2);plot(abs(Y));title(‘filterd signal’); subplot(3,1,3);plot(abs(H));title(‘filter frequency response’);
|
آزمایش نویز سفید:
چگالی طیفی نویز سفید در همه فرکانس‌ها یکسان است. بنابراین چگالی طیفی سیگنال خروجی فیلترشده هم شکل با پاسخ دامنه فیلتر است.
مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,
