جستجوی انتگرال معین برای استفاده در متلب

جستجوی انتگرال معین برای استفاده در متلب

به این مفهوم که، انتگرال معین ا ساساً حدی از جمع است، ما انتگرال معین را برای پیدا کردن مناطقی مانند مناطق بین  منحنی و محور x و منطقه بین دو منحنی  استفاده می کنیم. انتگرال معین همچنین می تواند در دیگر محل ها مورد استفاده قرار گیرد، که مقادیر مورد نیاز  می تواند به عنوان حدی از جمع بیان شود.

دستور int  می تواند برای ادغام  عبور حدها بر روی انتگرالی که شما می خواهید محاسبه کنیداستفاه شود.

برای محاسبه

می نویسیم،

برای مثال، برای محاسبه  می نویسیم:

int(x,4,9)

متلب دستورات بالا را اجرا خواهد کرد و نتیجه زیر را بازمی گرداند:

در زیر معادله octave محاسبات بالا است:

pkg load symbolic

symbols

x = sym(“x”):

f = x;

c = [1, 0] :

integral = polyint(c);

a = polyval(integral,9)- polyval(integral,4);

display(‘area: ‘), disp(double(a));

راه حل متناوب می تواند با استفاده از تابعquad()داده شده به صورت زیر فراهم شود:

pkg load symbolic

symbols

f =inline(“x”);

[a, ierror, nfneval]= quad(f,4,9);

display(‘area: ‘), disp(double(a));

مثال1

اجازه دهید محل در میان قرار گرفته شده در بین محورxو منحنیy=x³-2x+5 و عرض x=1و x=2 را محاسبه نماییم.

محل مورد نیاز به این صورت داده شده است:

یک فایل اسکریپت ایجاد کنید و کد زیر را تایپ نمایید:

f = x^3-2*x +5;

a =int (f, 1, 2)

display(‘area: ‘), disp(double(a));

زمانی که شما فایل را ایجاد می کنید، نتیجه زیر نمایش می یابد:

معادلهoctaveمحاسبات بالا در زیر آمده است:

pkg load symbolic

symbols

x = sym(“x”):

f = x^3-2*x +5;

c =[l,0,-2, 5]

integral = polyint(c);

a = polyval(integral,2)- polyval(integral,l);

display(‘area: ‘), disp(double(a));

راه حل متناوب می تواند با استفاده از تابع quad() داده شده octaveزیر را فراهم کند:

pkg load symbolic

symbols

x =   ( “x” ) ;

f =inline(“x^3 – 2*x +5”);

[a, ierror, nfneval]= quad(f,l,2);

display(‘area: ‘), disp(double(a));

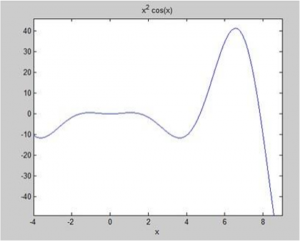
مثال 2

 ناحیه زیر منحنی پیدا می شود:f(x)=x²cos(x)for-4 .

یک فایل اسکریپت ایجاد کنید و کد زیر را تایپ نمایید:

f = x^2*cos(x);

ezplot(f,[-4,9])

a =int(f,-4,9)

disp(‘axea: ‘), disp(double(a));

زمانی که فایل را اجرا می کنید، متلب نمودار را رسم می کند:

و نتایج زیر نشان داده می شود:

a

8*cos(4) + l8*cos(9) + l4*sin(4) + 79*sin(9)

area:

0.3326

در زیر معادله octave محاسبات بالا است:

pkg load symbolic

symbols

x = sym(“x”);

f =inline(“x^2*cos(x)”);

ezplot(f,[—4,9])

print-deps gxaph.eps

[a, ierror, nfneval]= quad(f,-4,9);

display(‘area: ‘), disp(double(a));

نویسنده: مهندس عربعامری

 

مقاله متلب,مطلب,متلب,مقاله برق,مقاله قدرت,مقاله مطلب,مقاله سیمولینک,دانلود متلب,دانلود مقاله متلب,مقالهmatlab ,آموزش متلب,مطلب,متلب,آموزش برق,آموزش قدرت,آموزش مطلب,آموزش سیمولینک,دانلود متلب,دانلود آموزش متلب,آموزشmatlab ,پروژه متلب,مطلب,متلب,پروژه برق,پروژه قدرت,پروژه مطلب,پروژه سیمولینک,دانلود متلب,دانلود پروژه متلب,پروژهmatlab ,