آموزش نرم افزار متلب برای رشته برق – ایجاد ماتریس ها( بخش سوم)

آموزش نرم افزار متلب برای رشته برق – ایجاد ماتریس ها( بخش سوم)

ادامه بحث ایجاد ماتریس ها را با جمع دو ماتریس a و b دنبال می کنیم . برای مطالعه این بحث از ابتدا  ایجاد ماتریس ها( بخش اول) مراجعه نمایید.

جمع دو ماتریس a و b

c=a+b <<

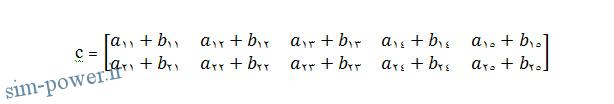
ماتریس c یک ماتریس (2⨯5) است .

اضافه کردن ستون

c=[a b] <<

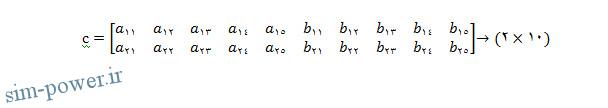
ماتریس c یک ماتریس (2⨯10) است .

اضافه کردن سطر

c=[a;b] <<

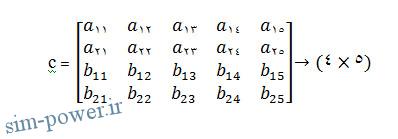
ماتریس c یک ماتریس (4⨯5) است .
علاوه بر این، اگر دو بردار بصورت x=[x1 x2 x3] و y=[y1 y2 y3] مفروض باشند، آنگاه z=[x ́ y ́] یا دستور z=[x;y] ماتریس زیر را ایجاد می کند:

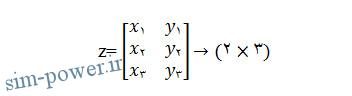
در صورتی که z=[x ́;y ́] باشد، نتیجه می دهد:

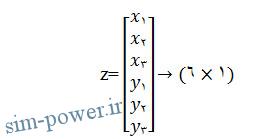
این روابط در هنگام جابجایی یک سری اطلاعات مشخص و ضروری بسیار مفید هستند.

مثال هایی از چگونگی تشکیل بردارها و ماتریس ها

یک ماتریس با وارد کردن المان هایش به طور یک جا تعریف می-شود. برای تعریف ماتریس A به صورت:

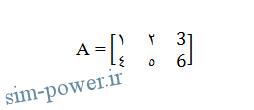
باید در خط فرمان عبارت زیر را وارد کرد:

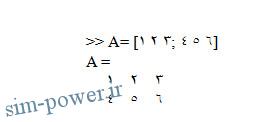
باید توجه داشت که از علامت ʺ ;ʺ برای جداسازی سطرها استفاده می شود. همانطور که قبلا بیان شد، برای جلوگیری از نمایش خروجی در انتهای دستور نیز از این علامت استفاده می شود. در صورتیکه ماتریس یا بردار برای المانهای زیادی باشد، استفاده از علامت ʺ ;ʺ در انتهای خط فرمان مهم است.
یک ماتریس، آرای های مستطیلی از اعداد است و دارای بردارهای ستونی و سطری می باشد. ماتریس ۴⨯۳ زیر را درنظر بگیرید.

این ماتریس را می­توان به صورت زیر در متلب سایت سیم پاور  وارد کرد:

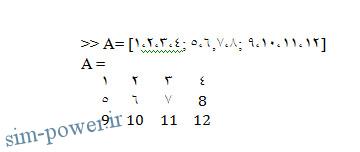
توجه کنید که عنصرها در هر سطر با علامت کاما (,) از هم جدا می شوند سطرها با علامت ; از یکدیگر جدا می شوند. همچنین همانگونه که در سایت سیم پاور  توضیح دادم عنصرها در هر سطر می توانند با فاصله از یکدیگر جدا شوند. ابعاد یک ماتریس با دستور size به دست می آید.

size(A) <<
ans =        3     4

چگونگی جمع ماتریسها

اگر دو ماتریس A و B هم اندازه باشند، مجموع آنها با تایپ A+B به دست می آید. همچنین همانگونه که در سایت سیم پاور  توضیح دادم می توان یک عدد تنها ( کمیت اسکالر) را با ماتریس جمع کرد. عبارت A+C مقدار C را به هر عنصر A اضافه می کند. همچنین همانگونه که در سایت سیم پاور  توضیح دادم A-B حاصل تفاضل دو ماتریس A و B را محاسبه می کند. A-C مقدار C را از همه عناصر A کم می کند.
ماتریس ترانهاده ماتریس حقیقی A توسط فرمان A ́ ایجاد می شود. اگر بردار سطری x به صورت زیر تعریف شود:

;x=[1 5 4 8 10] <<

سپس x توسط فرمان x ́ به یک بردار ستونی تبدیل می شود. در صورتیکه ماتریس یا بردار Z دارای عناصر مختلط باشد فرمان z ́ یک ماتریس ترانهاده ایجاد می کند که در اصل یک ماتریس ترانهاده به همراه مزدوج عناصر مختلط است. برای مثال :

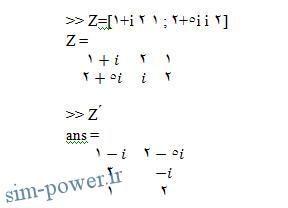
برای تشکیل ماتریس ترانهاده بدون مزدوج شدن عناصر مختلط از فرمان z ́ استفاده می شود. باید توجه داشت که یک نقطه قبل از علامت ( ́  ) قرار داده شود.
برای تعیین ابعاد یک بردار یا ماتریس، مثلا ماتریس A و بردار x که در بالا تعریف شد، از فرمان size به شکل زیر استفاده می شود:

 size(A) <<
ans =      3     4
size(x) <<
ans=   1     5
size(x ́) <<
ans=     5     1

همچنین همانگونه که در سایت سیم پاور  توضیح دادم می توان یک عنصر مشخص از یک بردار یا ماتریس را با مشخص کردن اندیس هایش به صورت زیر مشاهده کرد:

A(1,2) <<
ans=     2
x(5) <<
ans=   10

بردارها

…. بردارها و ماتریس هایی که مدنظر می باشند، دارای عناصر زیادی هستند و وارد کردن آنها به طور همزمان مشکل می باشد. در صورتی که رابطه خاص یا نظم خاصی بین عناصر ماتریس وجود داشته باشد از فرامین خاصی می توان استفاده کرد. برای مثال، برای وارد کردن بردار x شامل عناصر یا مولفه های (0,0.1,0.2,0.3,0.4,…,5.9,60 می توان از فرمان زیر استفاده کرد:

; x=0:0.1:6<<

این بردار سطری دارای 61 المان است. راه دیگری برای ایجاد برداری مشابه، استفاده از فرمان linspace است(مخفف Linear Space به معنی فواصل خطی می باشد):

 ;x=linspace(0,6,61) <<

این فرمان هنگامی قابل استفاده است که لازم است یک فاصله به تعدادی زیر فاصله با طول یکسان تقسیم شود.
برای مثال فرمان theta=inespace(0,2*pi,41) ، فاصله] [0, 2π را به 40 قسمت مساوی تقسیم می کند و یک بردار …. عضوی ایجاد می شود.
برای ایجاد بردارهای صفر و بردارهایی با عناصر یک با ابعادی مشابه ابعاد بردار اصلی x، از فرمان های زیر استفاده می شود:

;y=ones(size(x)) <<
;  y=ones(size(x))<<

این عمل را برای ماتریس ها نیز می توان انجام داد:

همچنین همانگونه که در سایت سیم پاور  توضیح دادم ماتریس های صفر و ماتریس های یک به صورت زیر و با مشخص کردن ابعاد تعریف می شوند:

یک ماتریس واحد n⨯n بوسیله فرمان eye(n) ایجاد می شود. فرامین ویژه ای نیز برای وارد کردن ماتریس های قطری و ماتریس های sparse وجود دارد. برای کسب اطلاعات بیشتر در این زمینه می توان این فرامین را وارد کرد:

help sparse <<
help diag <<

برای دانلود این آموزش به صورت پی دی اف بر روی لینک زیر کلیک کنید.

دانلود فایل ایجاد ماتریس ها( بخش سوم)